Cho tam giác BC. Từ một điểm M bất kì trong tam giác kẻ MD, ME, MF lần lượt vuông góc với các cạnh BC, CA, AB (h.8).
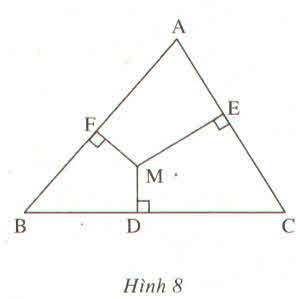
Chứng minh rằng :
\(BD^2+CE^2+AF^2=DC^2+EA^2+FB^2\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 9 2016
Kí hiệu như trên hình.
Ta có : \(AF^2+MF^2=AE^2+EM^2=AM^2\)
\(BD^2+MD^2=BF^2+MF^2=BM^2\)
\(ME^2+EC^2=MD^2+DC^2=MC^2\)
Cộng các đẳng thức trên theo vế
\(\left(BD^2+CE^2+AF^2\right)+\left(MF^2+MD^2+ME^2\right)=\left(DC^2+EA^2+FB^2\right)+\left(EM^2+MF^2+MD^2\right)\)
\(\Rightarrow BD^2+CE^2+AF^2=DC^2+EA^2+FB^2\)
2 tháng 12 2018
△DMC vuông tại D => DC2= MC2 - MD2
△AME vuông tại E => EA2 = AM2 - ME2
△BMF vuông tại F => BF2 = BM2 - MF2
Suy ra DC2 + EA2 + BF2 = MC2 - MD2 + AM2 - ME2 + BM2 - MF2 (1)
△BDM vuông tại D => BD^2 = BM^2 - MD^2
△CME vuông tại E => CE^2 = MC^2 - ME^2
△AMF vuông tại F => AF^2 = AM^2 - MF^2
Suy ra BD2 + CE2 + AF2 = BM2 - MD2 + MC2 - ME2 + AM2 - MF2 (2)
Từ (1) và (2) => BD2 + CE2 + AF2 = DC2 + EA2 + FB2
2 tháng 8 2020
Áp dụng định lí Pi-ta-go vào tam giác vuông BDM, ta có:
BM2 = BD2 + DM2 => BD2 = BM2 – DM2 (1)
Áp dụng định lí Pi-ta-go vào tam giác vuông CEM, ta có:
CM2 = CE2 + EN2 => CE2 = CM2 – EM2 (2)
Áp dụng định lí Pi-ta-go vào tam giác vuông AFM, ta có:
AM2 = AF2 + FM2 => AF2 = AM2 – FM2 (3)
Cộng từng vế của (1), (2) và (3) ta có:
BD2 + CE2 + AF2 = BM2 – DM2 + CM2 – EM2 + AM2 – FM2 (4)
Áp dụng định lí Pi-ta-go vào tam giác vuông BFM, ta có:
BM2 = BF2 + FM2 (5)
Áp dụng định lí Pi-ta-go vào tam giác vuông CDM, ta có:
CM2 = CD2 + DM2 (6)
Áp dụng định lí Pi-ta-go vào tam giác vuông AEM, ta có:
AM2 = AE2 + EM2 (7)
Thay (5), (6), (7) vào (4) ta có:
BD2 + CE2 + AF2
= BF2 + FM2 – DM2 + CD2 + DM2 – EM2 + AE2 + EM2 – FM2
= DC2 + EA2 + FB2
Vậy BD2 + CE2 + AF2 = DC2 + EA2 + FB2
15 tháng 9 2016
Bài 2.
Áp dụng định lí Pytago ta có :
\(AM^2=AF^2+FM^2=AE^2+ME^2\)
\(BM^2=BD^2+MD^2=MF^2+BF^2\)
\(MC^2=ME^2+EC^2=MD^2+DC^2\)
\(\Rightarrow AF^2+FM^2+BD^2+MD^2+ME^2+EC^2=AE^2+ME^2+MF^2+BF^2+MD^2+DC^2\)
\(\Rightarrow BD^2+CE^2+AF^2=DC^2+EA^2+FB^2\)
△DMC vuông tại D => DC2= MC2 - MD2
△AME vuông tại E => EA2 = AM2 - ME2
△BMF vuông tại F => BF2 = BM2 - MF2
Suy ra DC2 + EA2 + BF2 = MC2 - MD2 + AM2 - ME2 + BM2 - MF2 (1)
△BDM vuông tại D => BD^2 = BM^2 - MD^2
△CME vuông tại E => CE^2 = MC^2 - ME^2
△AMF vuông tại F => AF^2 = AM^2 - MF^2
Suy ra BD2 + CE2 + AF2 = BM2 - MD2 + MC2 - ME2 + AM2 - MF2 (2)
Từ (1) và (2) => BD2 + CE2 + AF2 = DC2 + EA2 + FB2
giỏi thật