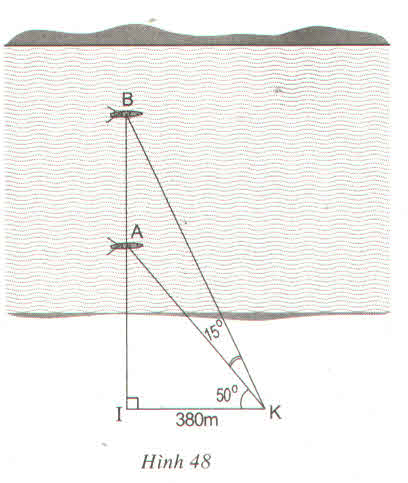
Hai chiếc thuyền A và B ở vị trí được minh họa như trong hình 48. Tính khoảng cách giữa chúng (làm tròn đến mét)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LH
Lưu Hạ Vy
24 tháng 4 2017
Đúng(0)
PT
Phan Thùy Linh
24 tháng 4 2017
Đúng(0)
Những câu hỏi liên quan
CM
28 tháng 7 2018
Trong tam giác vuông BIK có:
I B = I K . t g ∠ I K B = I K . t g ( 50 ° + 15 ° ) = 380 . t g 65 ° ≈ 814 ( m )
Trong tam giác vuông AIK có:
I A = I K . t g ∠ I K A = I K . t g 50 ° = 380 . t g 50 ° ≈ 452 ( m )
Vậy khoảng cách giữa hai thuyền là:
AB = IB – IA = 814 – 452 = 362 (m)
CM
27 tháng 7 2017
Trong tam giác vuông BIK có:
IB = IK.tg ∠IKB = IK.tg(50o + 15o) = 380.tg 65o ≈ 814 (m)
Trong tam giác vuông AIK có:
IA = IK.tg ∠IKA = IK.tg 50o = 380.tg50o ≈ 452 (m)
Vậy khoảng cách giữa hai thuyền là:
AB = IB – IA = 814 – 452 = 362 (m)
CM
12 tháng 9 2017
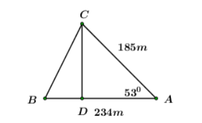
Từ C, dựng đường vuông góc với AB, cắt AB tại D.
Khi đó ta có: CD là đường cao của ABC.
Áp dụng tỉ số lượng giác của góc nhọn trong ACD vuông tại D ta có:
=> BD = AB – AD = 234 − 185. c o s 53 0
Áp dụng định lý Py-ta-go cho BCD để tính BC.
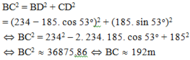
Đáp án cần chọn là: C
18 tháng 2 2021
Lấy C sao cho C, A, B thẳng hàng. Đặt giác kế tại C và lấy D sao cho góc DCA = 90°.
– Chuyển giác kế sang D và đo góc CDA = α ; CDB = β
– Đo CD = m
Ta có : ∆CAD có góc C = 90°, góc D = α, CD = m nên CA = m.tgα .
ACDB có góc C = 90°, CD = m, góc D = β nên CB = CD.tgD = m.tgβ .
=> AB = CB – CA = m.tgβ – m.tgα = m(tgβ – tgα).
Tham khảo :
HN
20 tháng 8 2021
Gọi chân hải đăng là A thì ta để ý thấy. Lần đầu quan sát thì tam giác DAB là nửa tam giác đều
\(\Rightarrow DA^2+AB^2=DB^2\)
\(\Leftrightarrow DA^2+AB^2=4AB^2\)
\(\Leftrightarrow DA^2=3AB^2=3.75^2=11250\)
\(\Leftrightarrow DA=106,066\)
Lần thứ 2 quan sát thì tam giác CAB là tam giác vuông cân
\(\Rightarrow CA=AB=75\)
Vậy quãng đường thuyền đi được là:
\(DC=DA-CA=106,066-75=31,066\)
2 tháng 12 2023
Gọi C là vị trí của máy bay
Gọi CH là độ cao của máy bay so với mặt đất
=>CH\(\perp\)AB tại H
Ta có hình vẽ sau:
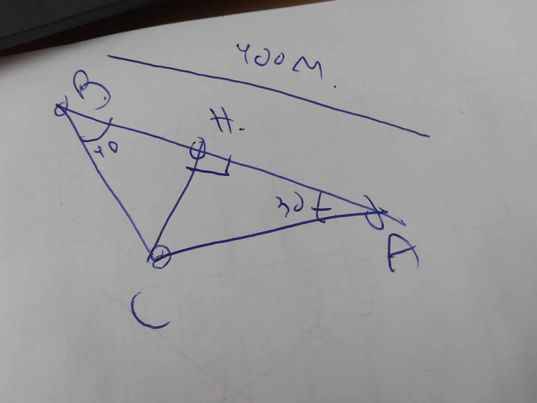
Xét ΔCBA có \(\widehat{CBA}+\widehat{CAB}+\widehat{ACB}=180^0\)
=>\(\widehat{ACB}+30^0+40^0=180^0\)
=>\(\widehat{ACB}=110^0\)
Xét ΔABC có \(\dfrac{BA}{sinACB}=\dfrac{AC}{sinB}=\dfrac{BC}{sinA}\)
=>\(\dfrac{400}{sin110}=\dfrac{AC}{sin40}=\dfrac{BC}{sin30}\)
=>\(AC\simeq273,62\left(m\right);BC\simeq212,84\left(m\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot CA\cdot CB\cdot sinACB\)
\(=\dfrac{1}{2}\cdot273,62\cdot212,84\cdot sin110\simeq27362,57\left(m^2\right)\)
Xét ΔACB có CH là đường cao
nên \(\dfrac{1}{2}\cdot CH\cdot AB=S_{ABC}\)
=>\(CH\cdot\dfrac{400}{2}=27362,57\)
=>\(CH\simeq136,81\left(m\right)\)