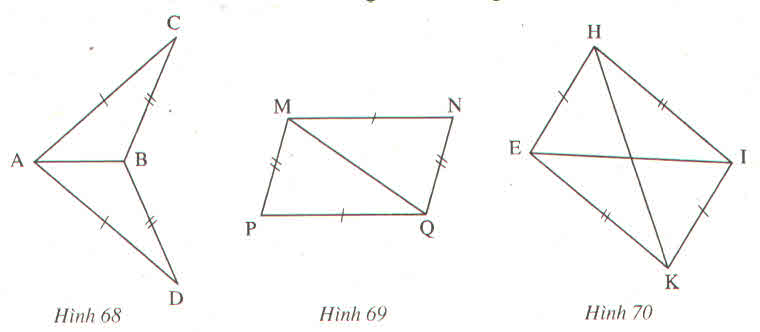
Trên mỗi hình 68, 69, 70 có các tam giác nào bằng nhau ? Vì sao ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
17 tháng 1 2019
- Hình 68
Xét tam giác ABC và tam giác ABD có:
AB = AB (cạnh chung)
AC = AD (gt)
BC = BD (gt)
Vậy ΔABC = ΔABD (c.c.c)
- Hình 69
Xét tam giác MNQ và tam giác QPM có:
MN = QP (gt)
NQ = PM (gt)
MQ cạnh chung
Vậy ΔMNQ = ΔQPM (c.c.c)
- Hình 70
Xét tam giác EHI và tam giác IKE có:
EH = IK (gt)
HI = KE (gt)
EI = IE (cạnh chung)
Vậy ΔEHI = ΔIKE (c.c.c)
Xét tam giác EHK và tam giác IKH có:
EH = IK (gt)
EK = IH (gt)
HK = KH (cạnh chung)
Vậy ΔEHK = ΔIKH (c.c.c)
PT
2
16 tháng 12 2020
in chào bạn. Tôi là Liana. Tôi đã **** trong một vụ tai nạn năm tôi 6 tuổi. Bạn phải đọc hết tin nhắn này nếu không bạn sẽ gặp xui xẻo cả đời.
Hiện tại thì tôi có thể đang ở rất gần bạn và tôi yêu cầu bạn phải chia sẻ tin nhắn này cho 20 người nữa. Nếu không làm được, bạn sẽ ****.
Ví dụ 1: Có một chàng trai tên là Meson, anh ấy đọc được tin nhắn này. Nhưng anh đã cười nhạo và không chia sẻ cho 20 người nên vào 2 giờ sáng, anh ấy đã *** do một vụ tai nạn. Một cái *** giống y hệt của tôi. Là tôi làm đấy!
Ví dụ 2: Một có gái trẻ tên là Alisean. Cô cũng nhận được dòng tin nhắn này nhưng cô chỉ chia sẻ cho 10 người và cô đã gặp ác mộng suốt phần đời còn lại
Thêm một ví dụ nữa: Có ba người bạn thân và họ tên là Tini Ly, Miin dukki và Anna An. Họ đang chơi đùa vui vẻ thì nhận được những dòng tin nhắn này và họ đã gửi ngay cho 20 người. Vậy là họ trở thành những con người may mắn. Họ được mọi người yêu quý, điểm số của họ cũng rất cao.
Vậy bạn muốn giống ai? Hãy gửi tiếp cho 20 người để được may mắn hoặc không thì bạn sẽ xui xẻo hoặc ****. Trò chơi sẽ bắt đầu từ lúc bạn đọc những dòng tin nhắn này. CHÚC BẠN MAY MẮN
PT
1
PT
1
CM
11 tháng 6 2017
+ Hình 82: ∆ADB = ∆ADE (c.g.c) vì :
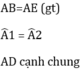
+ Hình 83: ∆HGK = ∆IKG (c.g.c) vì:
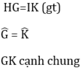
+ Hình 84: ∆PMQ và ∆PMN có:
Nhưng góc M không phải góc xen giữa nên ∆PMQ không bằng ∆PMN
PT
1
CM
13 tháng 12 2017
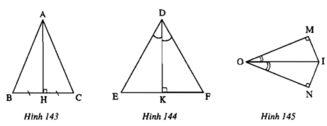
- hình 143 :
Xét tam giác ABH vuông tại H và tam giác ACH vuông tại H có:
AH chung
BH = CH (gt)
⇒ ΔABH =ΔACH (hai cạnh góc vuông)
- hình 144 :
Xét tam giác DEK vuông tại K và tam giác DFK vuông tại K có:
DK chung
∠(KDE) = ∠(KDF) (GT)
⇒ ΔDEK =ΔDFK (cạnh góc vuông – góc nhọn kề)
- hình 144 :
Xét tam giác OMI vuông tại M và tam giác ONI vuông tại N có:
OI chung
∠(MOI) = ∠(NOI) (GT)
⇒ ΔOMI = ΔONI (cạnh huyền – góc nhọn)
LM
1
PT
1
CM
31 tháng 5 2018
+ Hình 105: ΔABH và ΔACH cùng vuông tại H có:
BH = CH (gt)
AH cạnh chung
⇒ ΔABH = ΔACH (hai cạnh góc vuông)
+ Hình 106: Xét ΔDKE vuông tại K và ΔDKF vuông tại K có:
DK chung
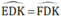
⇒ ΔDKE và ΔDKF (cạnh góc vuông – góc nhọn kề).
+ Hình 107: Xét ΔABD vuông tại B và ΔACD vuông tại C có:
AD chung
⇒ ΔABD = ΔACD (cạnh huyền – góc nhọn )
+ Hình 108:
• ΔABD = ΔACD (cạnh huyền – góc nhọn) (giống hình 107).
⇒ AB = AC và BD = CD (hai cạnh tương ứng)
• Xét ΔABH vuông tại B và ΔACE vuông tại C có
Góc A chung
AB = AC
⇒ΔABH = ΔACE (cạnh góc vuông – góc nhọn kề).
• Xét ΔDBE vuông tại B và ΔDCH vuông tại C có:
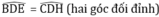
BD = DC (chứng minh trên)
⇒ ΔDBE = ΔDCH (cạnh góc vuông – góc nhọn kề)
H143
H144
H145
PT
5 tháng 2 2021
- hình 143 :
Xét tam giác ABH vuông tại H và tam giác ACH vuông tại H có:
AH chung
BH = CH (gt)
⇒ ΔABH =ΔACH (hai cạnh góc vuông)
- hình 144 :
Xét tam giác DEK vuông tại K và tam giác DFK vuông tại K có:
DK chung
∠(KDE) = ∠(KDF) (GT)
⇒ ΔDEK =ΔDFK (cạnh góc vuông – góc nhọn kề)
- hình 144 :
Xét tam giác OMI vuông tại M và tam giác ONI vuông tại N có:
OI chung
∠(MOI) = ∠(NOI) (GT)
⇒ ΔOMI = ΔONI (cạnh huyền – góc nhọn)
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
a) Xét 2 tam giác vuông ABC và ADC có:
\(\widehat {ACB} = \widehat {ACD}( = 90^\circ )\)
AC chung
\(\widehat {BAC} = \widehat {DAC}\)(gt)
=>\(\Delta ABC = \Delta ADC\)(g.c.g)
b) Xét 2 tam giác vuông HEG và GFH có:
HE=GF(gt)
HG chung
=>\(\Delta HEG = \Delta GFH\)(cạnh huyền - cạnh góc vuông)
c) Xét 2 tam giác vuông QMK và NMP có:
QK=NP(gt)
\(\widehat K = \widehat P\)(gt)
=>\(\Delta QMK = \Delta NMP\)(cạnh huyền – góc nhọn)
d) Xét 2 tam giác vuông VST và UTS có:
VS=UT(gt)
ST chung
=>\(\Delta VST = \Delta UTS\)(2 cạnh góc vuông)
Hình 68.
Xét \(\Delta ABC;\Delta ABD\):
AC = AD (gt)
AB chung
BC = BD (gt)
=> \(\Delta ABC=\Delta ABD\left(c.c.c\right)\)
Hình 69.
Xét \(\Delta MNQ;\Delta QPM:\)
MN = QP (gt)
MQ chung
NQ = PM (gt)
=> \(\Delta MNQ=\Delta QPM\left(c.c.c\right)\)
Hình 70. Gọi giao điểm của HK và EI là O.
Xét tg HEI; tg KIE:
EH = KI
EI chung
HI = KE
=> tg HEI = tg KIE (c.c.c)
=> g HEI = g KIE hay g HEO = g OIK
Tương tự: tg HIK = tg KEH (c.c.c)
=> g IHK = g EKH hay g IHO = g OKE
Xét tg HEO; tg KIO:
g HEO = g OIK (c/m trên)
HE = KI
g EHO = g OKI (cộng góc)
=> tg HEO = tg KIO (g.c.g)
Tương tự: tg HIO = tg KEO (g.c.g)