Cho em xin lời giải bài này ạ!!! Em cảm ơn 
K
Khách
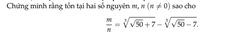
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AN
2
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 8 2021
\(y'=-3mx^2+2x-3\)
Hàm nghịch biến trên khoảng đã cho khi với mọi \(x\in\left(-3;0\right)\) ta có:
\(-3mx^2+2x-3\le0\)
\(\Leftrightarrow2x-3\le3mx^2\)
\(\Leftrightarrow\dfrac{2x-3}{3x^2}\le m\)
\(\Rightarrow m\ge\max\limits_{\left(-3;0\right)}\left(\dfrac{2x-3}{3x^2}\right)\)
Xét hàm \(f\left(x\right)=\dfrac{2x-3}{3x^2}\Rightarrow f'\left(x\right)=\dfrac{2\left(3-x\right)}{3x^3}< 0;\forall x\in\left(-3;0\right)\)
\(\Rightarrow f\left(x\right)>f\left(-3\right)=-\dfrac{1}{3}\)
\(\Rightarrow m\ge-\dfrac{1}{3}\)
HH
3
HQ
Hà Quang Minh
Giáo viên
16 tháng 8 2023
\(a,\dfrac{x}{9}=\dfrac{5}{3}\\ \Leftrightarrow x=9\cdot\dfrac{5}{3}\\ \Leftrightarrow x=15\\ b,\dfrac{17}{x}=\dfrac{85}{105}\\ \Leftrightarrow x=17\cdot\dfrac{105}{85}\\ \Leftrightarrow x=21\\ c,\dfrac{x}{8}+\dfrac{2}{3}=\dfrac{7}{6}\\ \Leftrightarrow\dfrac{x}{8}=\dfrac{1}{2}\\ \Leftrightarrow x=4\\ d,\dfrac{3}{x-7}=\dfrac{27}{135}\\ \Leftrightarrow x-7=15\\ \Leftrightarrow x=22\)
HQ
Hà Quang Minh
Giáo viên
16 tháng 8 2023
\(e,\dfrac{75}{20-x}=\dfrac{3}{2}\times10\\ \Leftrightarrow\dfrac{75}{20-x}=15\\ \Leftrightarrow20-x=5\\ \Leftrightarrow x=15\\ f,\left(x-50\%\right)\times\dfrac{5}{3}=\dfrac{7}{4}-0,5\\ \Leftrightarrow\left(x-\dfrac{1}{2}\right)\times\dfrac{5}{3}=\dfrac{5}{4}\\ \Leftrightarrow x-\dfrac{1}{2}=\dfrac{3}{4}\\ \Leftrightarrow x=\dfrac{5}{4}\\ g,\left(\dfrac{2}{15}+\dfrac{3}{35}+\dfrac{2}{63}\right):x=\dfrac{1}{18}\\ \Leftrightarrow\dfrac{2}{9}:x=\dfrac{1}{18}\\ \Leftrightarrow x=4\)
\(h,\left[\left(x-\dfrac{1}{2}\right):6+4\right]\times\dfrac{2}{3}=0,6\times\dfrac{40}{6}\\ \Leftrightarrow\left[\left(x-\dfrac{1}{2}\right):6+4\right]\times\dfrac{2}{3}=4\\ \Leftrightarrow\left(x-\dfrac{1}{2}\right):6+4=6\\ \Leftrightarrow\left(x-\dfrac{1}{2}\right):6=2\\ \Leftrightarrow x-\dfrac{1}{2}=12\\ \Leftrightarrow x=\dfrac{25}{2}\)
F
17 tháng 4 2022
\(y=\dfrac{sinx-cosx}{sinx+cosx}\Rightarrow y'=\dfrac{\left(sinx-cosx\right)'.\left(sinx+cosx\right)-\left(sinx+cosx\right)'.\left(sinx-cosx\right)}{\left(sinx+cosx\right)^2}\)
Dễ thấy : \(\left(sinx-cosx\right)'=cosx+sinx\)
\(\left(sinx+cosx\right)'=cosx-sinx\)
Suy ra : \(y'=\dfrac{\left(sinx+cosx\right)^2+\left(sinx-cosx\right)^2}{\left(sinx+cosx\right)^2}=\dfrac{2}{\left(sinx+cosx\right)^2}\)
8 tháng 7 2023
a: góc BDO+góc OMB=90+90=180 độ
=>BDOM nội tiếp
góc BCE=góc CAE
góc DOM+góc MBD=180 độ
góc MBD=góc NAE
=>góc DOM+góc NAE=180 độ
b: OD vuông góc BE
=>D là trung điểm của BE
ΔBEC có MD là đường trung bình
=>MD//EC
=>DF//CE
DF//CE
=>ΔNFD đồng dạng với ΔNCE
=>NF/NC=ND/NE
=>NF*NE=NC*ND
9 tháng 4 2022
a: Phương trình hoành độ giao điểm là:
\(-x^2-2mx+m^2-4=0\)
\(\text{Δ}=\left(-2m\right)^2-4\cdot\left(-1\right)\cdot\left(m^2-4\right)=4m^2+4\left(m^2-4\right)=4m^2+4m^2-16=8m^2-16\)
=>Đề sai rồi bạn
YL
0
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
22 tháng 8 2023
a) x - 15 x 7 - 270 : 45 = 169
x- 105 - 6 = 169
x = 169 + 6 + 150
x = 325
b)[(4x + 28 ) x 3 + 55 ] : 5 = 35
[12x + 84 + 55 ] = 35 x 5
12x + 139 = 175
12x = 175 - 139
12x = 36
x = 36 : 12
x = 3
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
22 tháng 8 2023
c)(455 - x : 2 x 6) : 5 = 31
455 - x : 2 x 6 = 31 x 5
455 - x : 2 x6 = 155
x : 2 x 6 = 455 - 155
x : 2 x6 = 300
x : 2 = 300 : 6
x: 2 = 50
x = 50 x 2
x= 100
Đặt \(x=\sqrt[3]{\sqrt[]{50}+7}-\sqrt[3]{\sqrt[]{50}-7}\)
\(x^3=14-3\sqrt[3]{\left(\sqrt[]{50}+7\right)\left(\sqrt[]{50}-7\right)}\left(\sqrt[3]{\sqrt[]{50}+7}-\sqrt[3]{\sqrt[]{50}-7}\right)\)
\(x^3=14-3x\)
\(x^3+3x-14=0\)
\(\left(x-2\right)\left(x^2+2x+7\right)=0\)
\(x=2\)
\(\Rightarrow\dfrac{m}{n}=2\)
\(\Rightarrow\) Hiển nhiên tồn tại vô số m, n nguyên thỏa mãn đẳng thức trên