Xét trường hợp đoạn mạch có điện trở R, hãy chứng tỏ rằng công suất điện của đoạn mạch được tính theo công thức
\(P=I^2R=\dfrac{U^2}{R}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhiệt lượng của đoạn mạch tỏa ra khi có dòng điện chạy qua là: Q=UIt
Mà: \(R=\dfrac{U}{I}\Rightarrow Q=I^2Rt=\dfrac{U^2}{R}\cdot t\)

Nếu mạch ngoài chỉ có điện trở thuần:
Ta có: UN = I.RN và E = I.(RN + r)
Hiệu suất của nguồn điện khi này:
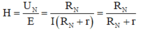

Công suất P là đại lượng đặc trưng cho tốc độ thực hiện công, được tính bằng công thực hiện được trong một đơn vị thời gian: P= A/t → A = P.t
Mà P = UI. Vậy A = UIt.

Chọn D. Điện năng mà đoạn mạch này tiêu thụ trong khoảng thời gian t được tính theo công thức A = UIt

Đáp án B
+ Hệ số công suất như nhau nên
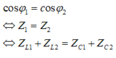
+ Mặc khác ta lại có
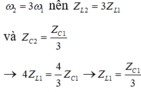
+ Vì uAM vuông pha với u M B nên
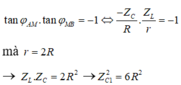
+ Hệ số công suất của đoạn mạch là:


Nhiệt năng sinh ra trong khoảng thời gian đó là:
\(Q=I^2Rt\)
Năng lượng tiêu thụ được chuyển hóa thành nhiệt năng:
\(A=Pt\)
Do năng lượng điện tiêu thụ được chuyển hoá hoàn toàn thành nhiệt nên:
\(Q=A\Rightarrow I^2Rt=Pt\)
Suy ra công suất tỏa nhiệt là:
\(P_{hp}=I^2R\)

Chọn B. P = U/I vì công suất tiêu thụ điện năng P = U.I = I 2 R = U 2 / R nên đáp án B sai
Trường hợp đoạn mạch có điện trở R, ta có P = UI mà U = IR, suy ra P = IR.I = I2R.
Mặt khác, ta có P = UI, mà I =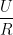 => p = U.
=> p = U.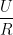 =
= 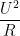 .
.