Cho a, b, c là 3 cạnh của tam giác. Chứng minh:
\(\dfrac{ab}{a+b-c}+ \dfrac{bc}{b+c-a}+ \dfrac{ca}{c+a-b} \geq a+b+c\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2020
\(\Leftrightarrow ab\left(\dfrac{1}{b+c}-\dfrac{1}{a+c}\right)+bc\left(\dfrac{1}{a+c}-\dfrac{1}{a+b}\right)+ca\left(\dfrac{1}{a+b}-\dfrac{1}{b+c}\right)=0\)
\(\Leftrightarrow\dfrac{ab\left(a-b\right)}{\left(b+c\right)\left(a+c\right)}+\dfrac{bc\left(b-c\right)}{\left(a+b\right)\left(a+c\right)}+\dfrac{ca\left(c-a\right)}{\left(a+b\right)\left(b+c\right)}=0\)
\(\Leftrightarrow\dfrac{ab\left(a^2-b^2\right)+bc\left(b^2-c^2\right)+ca\left(c^2-a^2\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=0\)
\(\Leftrightarrow\dfrac{\left(a-b\right)\left(b-c\right)\left(a-c\right)\left(a+b+c\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=b\\b=c\\c=a\end{matrix}\right.\) hay tam giác cân
HN
27 tháng 4 2017
Gọi cái đó là P
Đặt \(\left\{{}\begin{matrix}b+c-a=2x\\c+a-b=2y\\a+b-c=2z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=y+z\\b=z+x\\c=x+y\end{matrix}\right.\)
Thì ta có:
\(P=\dfrac{\left(x+z\right)\left(y+z\right)}{2z}+\dfrac{\left(x+y\right)\left(z+y\right)}{2y}+\dfrac{\left(z+x\right)\left(y+x\right)}{2x}\ge2\left(x+y+z\right)\)
\(\Leftrightarrow2x^2y^2+2y^2z^2+2z^2x^2-2xyz^2-2yzx^2-2zxy^2\ge0\)
\(\Leftrightarrow\left(xy-yz\right)^2+\left(yz-zx\right)^2+\left(zx-xy\right)^2\ge0\) (đúng)
\(\RightarrowĐPCM\)
AT
7 tháng 6 2021
a) \(1+tan^2B=1+\dfrac{AC^2}{AB^2}=\dfrac{AB^2+AC^2}{AB^2}=\dfrac{BC^2}{AB^2}=\dfrac{1}{\left(\dfrac{AB}{BC}\right)^2}=\dfrac{1}{cos^2B}\)
b) Ta có: \(a.sinB.cosB=BC.\dfrac{AC}{BC}.\dfrac{AB}{BC}=\dfrac{AC.AB}{BC}=\dfrac{AH.BC}{BC}=AH\)
\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=BC.\left(\dfrac{AB}{BC}\right)^2=BC.cos^2B\)
Tương tự \(\Rightarrow CH=BC.sin^2B\)
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 12 2020
\(VT=\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}=\dfrac{a^2}{ab+ac}+\dfrac{b^2}{bc+ab}+\dfrac{c^2}{ac+bc}\)
\(VT\ge\dfrac{\left(a+b+c\right)^2}{2\left(ab+bc+ca\right)}\ge\dfrac{3\left(ab+bc+ca\right)}{2\left(ab+bc+ca\right)}=\dfrac{3}{2}\)
Dấu "=" xảy ra khi và chỉ khi \(a=b=c\)
\(\Rightarrow\) Tam giác là tam giác đều
A
26 tháng 1 2021
+ 
+ 
≥ 3.
Đặt b + c – a = x > 0 (1); a + c – b = y > 0 (2); a + b – c = z > 0 (3)
Cộng (1) và (2) => b + c – a + a + c – b = x + y ⇔ 2c = x + y ⇔ c =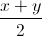 
Tương tự a =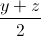 
; b =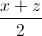 
Do đó + + = 
+ 
+ 
= 
(
+ 
+ 
+ 
+ 
+ 
)
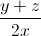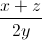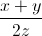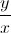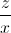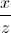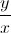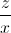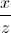= [( + ) + ( + ) + ( + )] ≥ (2 + 2 + 2) = 3.
Vậy + + ≥ 3.
đặt\(\left\{{}\begin{matrix}a+b-c=x\\b+c-a=y\\c+a-b=z\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=\dfrac{x+z}{2}\\b=\dfrac{x+y}{2}\\c=\dfrac{y+z}{2}\end{matrix}\right.\)
sau đó thay vào bt rồi tính là ra