Hai đỉnh của một khối 8 mặt đều cho trước gọi là các đỉnh đối diện nếu chúng không cùng thuộc một cạnh của khối đó. Đoạn thẳng nối hai đỉnh đối diện gọi là đường chéo của khối 8 mặt đều. Chứng minh rằng trong khối 8 mặt đều:
a/ Ba đường chéo cắt nhau tại trung điểm của mỗi đường.
b/ Ba đường chéo đối một vuông góc.
c/ Ba đường chéo bằng nhau


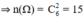
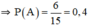
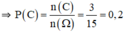

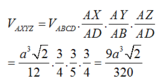
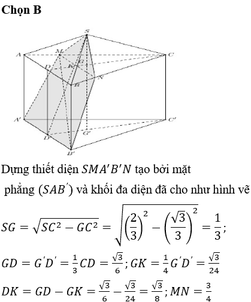
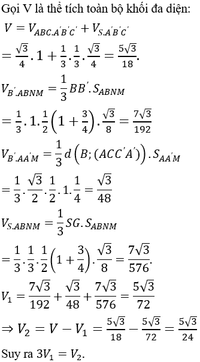

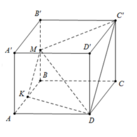
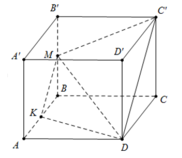

Giả sử SABCDS1 là khối 88 mặt đều.
a) Nhận xét rằng:
BA = BC ⇒ B thuộc mặt phẳng trung trực của AC.
DA = DC ⇒ D thuộc mặt phẳng trung trực của AC.
SA = SC ⇒ S thuộc mặt phẳng trung trực của AC.
S1A=S1C ⇒ B thuộc mặt phẳng trung trực của AC.
Từ đó suy ra B, D, S, S1 đồng phẳng và tứ giác SBS1D là hình thoi nên SS1 và BD cắt nhau tại trung điểm mỗi đường (giả sử O).
Chứng minh tương tự, ta có: AC và BD cắt nhau tại trung điểm mỗi đường.
Vậy, ba đường chép của khối 88 mặt đều cắt nhau tại trung điểm của mỗi đường (đpcm)
b) Từ kết quả câu a), vì SBS1D và ABCD là hình thoi nên các đường chéo vuông góc với nhau (đpcm)
c) Ta có:
ΔSAC = ΔBAC (c - c - c) ⇒ SO = BO (1)
ΔSBD = ΔABD (c - c - c) ⇒ SO = AO (2)
Từ đó suy ra AC = BD = SS1(đpcm).
Câu c Cm theo cách này đc k?#
Vì EO \(\perp\) (ABCD)
nên OA ; OB lần lượt là hình chiếu của EA; EB trên (ABCD)
mà EA = EB => OA = OB => AC = BD (1)
Cm tương tự: AC = EF (2)
Từ (1),(2) => AC = BD = EF