Tìm tọa độ điểm M' đối xứng với điểm M (1;4) qua đường thẳng d: x - 2y + 2 =0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


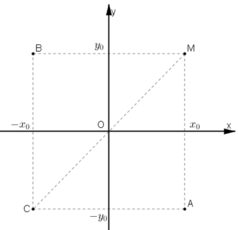
Biểu diễn các điểm trên hệ trục tọa độ ta thấy:
a) Điểm đối xứng với M(x0; y0) qua trục Ox là A(x0 ; –y0)
b) Điểm đối xứng với M(x0 ; y0) qua trục Oy là B(–x0 ; y0)
c) Điểm đối xứng với M(x0 ; y0) qua gốc O là C(–x0 ; –y0).

a: A(2;4); B(1;0); C(2;2)
vecto AB=(-1;-4)
vecto DC=(2-x;2-y)
Vì ABCD là hình bình hành nên vecto AB=vecto DC
=>2-x=-1 và 2-y=-4
=>x=3 và y=6
c: N đối xứng B qua C
=>x+1=4 và y+0=4
=>x=3 và y=4

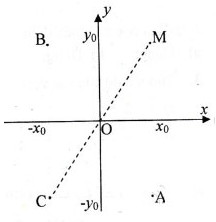
a) Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau và tung độ đối nhau.
M0 (x0; y0)=> A(x0;-y0)
b) Hai điểm đối xứng với nhau qua trục tung thì có tung độ bằng nhau còn hoành độ thì đối nhau.
M0 (x0; y0) => B(-x0;y0)
c) Hai điểm đối xứng nhau qua gốc O thì các tọa độ tương ứng đối nhau.
M0 (x0; y0) => C(-x0;-y0)

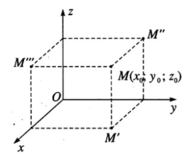
Gọi M’, M’’, M’’’ lần lượt là hình chiếu vuông góc của điểm M trên các mặt phẳng (Oxy), (Oyz), (Ozx).
Ta có:
• M’( x 0 ; y 0 ; 0)
• M’’ (0; y 0 ; z 0 )
• M’’’( x 0 ; 0; z 0 )


Đáp án C.
Chú ý rằng số phức z = 3 + 5 i được biểu diễn bởi điểm M a ; b trên mặt phẳng tọa độ.

a: Khi m=3 thì (d): y=2x+3
Phương trình hoành độ giao điểm là:
\(x^2-2x-3=0\)
=>(x-3)(x+1)=0
=>x=3 hoặc x=-1
Khi x=3 thì y=9
Khi x=-1 thì y=1
b: Phương trình hoành độ giao điểm là:
\(x^2-2x-m=0\)
Δ=4+4m
Để (P) tiếp xúc với (d) thì 4m+4=0
hay m=-1
Khoảng cách M đến d là: h=I1-2.4+2I/căn 5 =5/can5=căn5
M"(a,b) phải thuộc đường thẳng (d1) vuông góc với d:x-2y+2=0
d1: đi qua M' => d1: 2(x-1)+(y-4) =2x+y-6=0
=> 2a+b-6=0=> b=6-2a
Khoảng cách M" đến d là
h=I1-2.4+2I/căn 5 =5/can5=căn5
Khoảng cách từ M' đến d =căn5
=> Ia-2(6-2a)+2I =5 => I10+5aI=5
a=-1 hoặc a=3
M' khác phía với M qua d
=> M(3,0)