Tính \(A=\dfrac{-1}{3}+\dfrac{-1}{15}+\dfrac{-1}{35}+...+\dfrac{-1}{9999}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(M=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{2}{35}+\dfrac{2}{63}+...+\dfrac{2}{9603}+\dfrac{2}{9999}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{97}-\dfrac{1}{99}+\dfrac{1}{99}-\dfrac{1}{101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{2}\cdot\dfrac{96}{505}=\dfrac{150}{101}\)

\(\dfrac{1}{3}+\dfrac{13}{15}+\dfrac{33}{35}+...+\dfrac{9997}{9999}\)
\(=1-\dfrac{2}{3}+1-\dfrac{2}{15}+1-\dfrac{2}{35}+...+1-\dfrac{2}{9999}\)
\(=\left(1+1+1+...+1\right)-\dfrac{2}{3}+\dfrac{2}{15}+...+\dfrac{2}{9999}\)
\(=50-1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{101}\)
\(=50-\left(1-\dfrac{1}{101}\right)=50-\dfrac{100}{101}\)
\(=\dfrac{4950}{101}\)

a: \(M=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}+\dfrac{2}{99\cdot101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{10}-\dfrac{3}{202}=\dfrac{150}{101}\)
b: 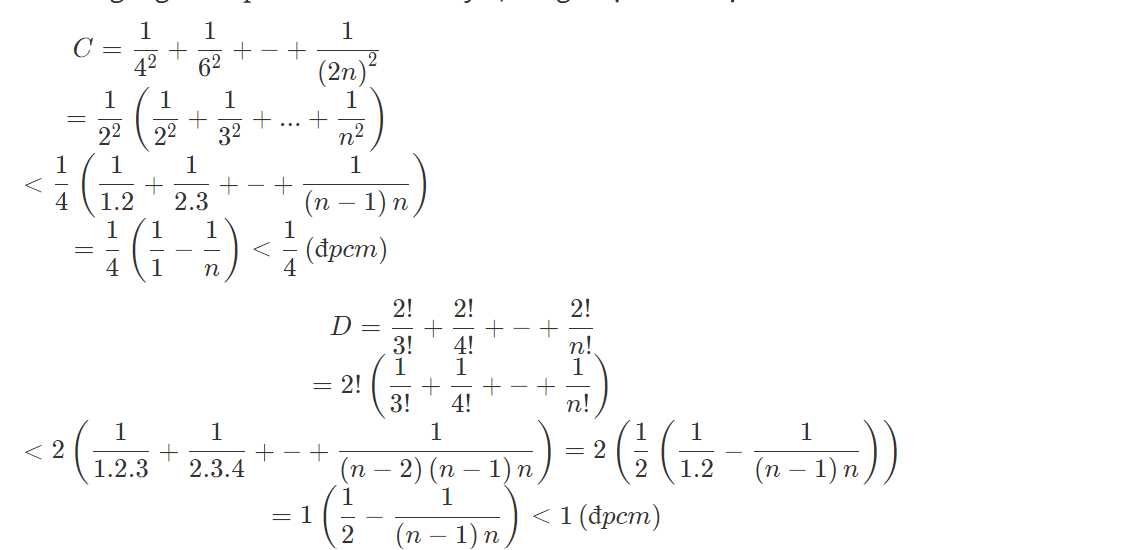

a,
\(\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2006}}\\ =1\cdot\left(\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2006}}\right)\\ =\left(2-1\right)\left(\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2006}}\right)\\ =\left(2-1\right)\cdot\dfrac{1}{2^2}+\left(2-1\right)\cdot\dfrac{1}{2^3}+...+\left(2-1\right)\cdot\dfrac{1}{2^{2006}}\\ =\dfrac{1}{2}-\dfrac{1}{2^2}+\dfrac{1}{2^2}-\dfrac{1}{2^3}+...+\dfrac{1}{2^{2005}}-\dfrac{1}{2^{2006}}\\ =\dfrac{1}{2}-\dfrac{1}{2^{2006}}\\ =\dfrac{2^{2005}}{2^{2006}}-\dfrac{1}{2^{2006}}\\ =\dfrac{2^{2005}-1}{2^{2006}}\)
b,
\(\dfrac{2}{5\cdot7}+\dfrac{2}{7\cdot9}+...+\dfrac{2}{59\cdot61}\\ =\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{59}-\dfrac{1}{61}\\ =\dfrac{1}{5}-\dfrac{1}{61}\\ =\dfrac{56}{305}\)
c,
\(\dfrac{7}{3}+\dfrac{7}{15}+\dfrac{7}{35}+...+\dfrac{7}{9999}\\ =\dfrac{7}{2}\cdot\left(\dfrac{2}{3}+\dfrac{2}{15}+\dfrac{2}{35}+...+\dfrac{2}{9999}\right)\\ =\dfrac{7}{2}\cdot\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{99\cdot101}\right)\\ =\dfrac{7}{2}\cdot\left(\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{101}\right)\\ =\dfrac{7}{2}\cdot\left(1-\dfrac{1}{101}\right)\\ =\dfrac{7}{2}\cdot\dfrac{100}{101}\\ =\dfrac{350}{101}\)
Đặt:
\(X=\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2006}}\)
\(2X=2\left(\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2006}}\right)\)
\(2X=\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2005}}\)
\(2X-X=\left(\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2005}}\right)-\left(\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2016}}\right)\)\(X=\dfrac{1}{2}-\dfrac{1}{2^{2016}}\)
\(Y=\dfrac{2}{5.7}+\dfrac{2}{7.9}+\dfrac{2}{9.11}+...+\dfrac{2}{59.61}\)
\(Y=\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{11}+...+\dfrac{1}{59}-\dfrac{1}{61}\)
\(Y=\dfrac{1}{5}-\dfrac{1}{61}=\dfrac{56}{305}\)
\(Z=\dfrac{7}{3}+\dfrac{7}{15}+\dfrac{7}{35}+...+\dfrac{7}{9999}\)
\(Z=\dfrac{7}{1.3}+\dfrac{7}{3.5}+\dfrac{7}{5.7}+...+\dfrac{7}{99.101}\)
\(Z=\dfrac{7}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{101}\right)\)
\(Z=\dfrac{7}{2}\left(1-\dfrac{1}{101}\right)\)
\(Z=\dfrac{7}{2}.\dfrac{100}{101}=\dfrac{700}{202}\)

a=78/35
b=22/12
c=1/1
d=40202090/4040090
e=1,24025667172...
f=871,82
ko biết đúng ko [0_0'] hihi

\(G=\dfrac{2}{5.8}+\dfrac{2}{8.11}+...+\dfrac{2}{95.98}+\dfrac{2}{98.101}\)
\(\Rightarrow G=\dfrac{2}{3}.\left(\dfrac{3}{5.8}+\dfrac{3}{8.11}+...+\dfrac{3}{95.98}+\dfrac{3}{98.101}\right)\)
\(\Rightarrow G=\dfrac{2}{3}.\left(\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+...+\dfrac{1}{95}-\dfrac{1}{98}+\dfrac{1}{98}-\dfrac{1}{101}\right)\)
\(\Rightarrow G=\dfrac{2}{3}.\left(\dfrac{1}{5}-\dfrac{1}{101}\right)\)
\(\Rightarrow G=\dfrac{2}{3}.\dfrac{96}{505}\)
\(\Rightarrow G=\dfrac{64}{505}\)

\(E=\dfrac{\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)\cdot...\cdot\left(\dfrac{1}{2002}-1\right)\left(\dfrac{1}{2003}-1\right)}{\dfrac{3}{4}\cdot\dfrac{8}{9}\cdot...\cdot\dfrac{9999}{10000}}\)
\(=\dfrac{\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\cdot...\cdot\left(1-\dfrac{1}{2002}\right)\left(1-\dfrac{1}{2003}\right)}{\left(1-\dfrac{1}{4}\right)\left(1-\dfrac{1}{9}\right)\left(1-\dfrac{1}{100^2}\right)}\)
\(=\dfrac{\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\cdot...\cdot\left(1-\dfrac{1}{2002}\right)\left(1-\dfrac{1}{2003}\right)}{\left(1-\dfrac{1}{2}\right)\left(1+\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\left(1+\dfrac{1}{3}\right)\cdot...\cdot\left(1-\dfrac{1}{100}\right)\left(1+\dfrac{1}{100}\right)}\)
\(=\dfrac{\dfrac{100}{101}\cdot\dfrac{101}{102}\cdot...\cdot\dfrac{2002}{2003}}{\left(1+\dfrac{1}{2}\right)\left(1+\dfrac{1}{3}\right)\cdot...\cdot\left(1+\dfrac{1}{100}\right)}\)
\(=\dfrac{100}{2003}:\left(\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{101}{100}\right)\)
\(=\dfrac{100}{2003}:\left(\dfrac{101}{2}\right)=\dfrac{100}{2003}\cdot\dfrac{2}{101}=\dfrac{200}{202303}\)

a) Sửa tí: \(1+\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2006}}\)
Đặt \(A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2006}}\)
\(\Rightarrow2A=2.\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2006}}\right)\)
\(\Rightarrow2A=2+1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2005}}\)
\(\Rightarrow2A-A=2+1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2005}}-\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2006}}\right)\)
\(\Rightarrow A=2+1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2005}}-1-\dfrac{1}{2}-\dfrac{1}{2^2}-\dfrac{1}{2^3}-...-\dfrac{1}{2^{2006}}\)
\(\Rightarrow A=2-\dfrac{1}{2^{2006}}\)
b) Đặt \(A=\dfrac{2}{5.7}+\dfrac{2}{7.9}+\dfrac{2}{9.11}+...+\dfrac{1}{50.61}\)
\(A=\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-...+\dfrac{1}{59}-\dfrac{1}{61}\)
\(A=\dfrac{1}{5}-\dfrac{1}{61}\)
\(A=\dfrac{56}{305}\)
c) Đặt \(A=\dfrac{7}{3}+\dfrac{7}{15}+\dfrac{7}{35}+...+\dfrac{7}{9999}\)
\(A=\dfrac{7}{2}.2.\left(\dfrac{1}{3}+\dfrac{1}{5}+...+\dfrac{1}{9999}\right)\)
\(A=\dfrac{7}{2}.\left(1-\dfrac{1}{101}\right)\)
\(A=\dfrac{7}{2}.\dfrac{100}{101}\)
\(A=\dfrac{256}{101}\)
\(A=\dfrac{-1}{3}+\dfrac{-1}{15}+\dfrac{-1}{35}+...+\dfrac{-1}{9999}\)
\(\Rightarrow-A=\dfrac{1}{3}+\dfrac{1}{15}+\dfrac{1}{35}+...+\dfrac{1}{9999}\)
\(-A=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{99.101}\)
\(-2A=\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{99.101}\)
\(-2A=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{101}\)
\(-2A=1-\dfrac{1}{101}\)
\(-2A=\dfrac{100}{101}\)
\(-A=\dfrac{100}{101}:2\)
\(-A=\dfrac{50}{101}\)
\(\Rightarrow A=\dfrac{-50}{101}\)
Chúc bạn học tốt!
\(A=\dfrac{-1}{3}+\dfrac{-1}{15}+\dfrac{-1}{35}+...+\dfrac{-1}{9999}\)
\(A=-\left(\dfrac{1}{3}+\dfrac{1}{15}+\dfrac{1}{35}+...+\dfrac{1}{9999}\right)\)
Đặt \(B=\dfrac{1}{3}+\dfrac{1}{15}+\dfrac{1}{35}+....+\dfrac{1}{9999}\)
\(B=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{99.101}\)
\(2B=\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{99.101}\)
\(2B=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{101}\)
\(2B=1-\dfrac{1}{101}=\dfrac{100}{101}\)
\(B=\dfrac{100}{101}:2=\dfrac{50}{101}\)
\(\Rightarrow A=-B=-\dfrac{50}{101}\)