Giải chi tiết giúp mình nhé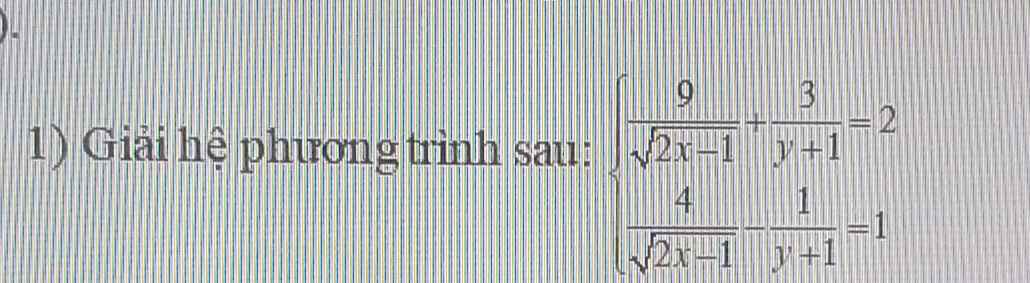
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 7 2021
Bài 18
a, Với \(a>0;a\ne1;4\)
\(A=\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)
\(=\left(\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}\right):\left(\dfrac{a-1-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\right)\)
\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{3}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)
b, Thay a = 9 => căn a = 3
\(A=\dfrac{3-2}{3.3}=\dfrac{1}{9}\)
c, Ta có : \(A.B=\dfrac{\sqrt{a}-2}{3\sqrt{a}}.\dfrac{3\sqrt{a}}{\sqrt{a}+1}=\dfrac{\sqrt{a}-2}{\sqrt{a}+1}< 0\)
Vì \(\sqrt{a}+1>\sqrt{a}-2\)
\(\left\{{}\begin{matrix}\sqrt{a}+1>0\\\sqrt{a}-2< 0\end{matrix}\right.\Leftrightarrow a< 4\)
Kết hợp với đk vậy \(0< a< 4;a\ne1\)
25 tháng 7 2021
Bài 18:
1) Ta có: \(A=\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)
\(=\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{a-1-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}{3}\)
\(=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)
2) Thay a=9 vào B, ta được:
\(B=\dfrac{3\cdot3}{3+1}=\dfrac{9}{4}\)
25 tháng 7 2021
a, \(A=\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\)ĐK : \(x>0;x\ne1\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}+1}=\dfrac{\sqrt{x}-1}{\sqrt{x}}\)
b, \(A=\dfrac{1}{3}\Rightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}}=\dfrac{1}{3}\Rightarrow3\sqrt{x}-3=\sqrt{x}\Leftrightarrow2\sqrt{x}=3\)
\(\Leftrightarrow\sqrt{x}=\dfrac{3}{2}\Leftrightarrow x=\dfrac{9}{4}\)
c, \(P=\dfrac{\sqrt{x}-1}{\sqrt{x}}-9\sqrt{x}=\dfrac{\sqrt{x}-1-9x}{\sqrt{x}}\)
\(=1-\dfrac{1}{\sqrt{x}}-9\sqrt{x}\)Đặt \(\sqrt{x}=t^2\left(t>0\right)\)
\(1-t-9t^2=-\left(9t^2-t-1\right)=-\left(9t^2-2.3.\dfrac{1}{6}.t+\dfrac{1}{36}-\dfrac{37}{36}\right)\)
\(=-\left(3t-\dfrac{1}{6}\right)+\dfrac{37}{36}\le\dfrac{37}{36}\)
Dấu ''='' xảy ra khi t = 1/18 => t^2 = 1/324 => \(\sqrt{x}=\dfrac{1}{324}\Rightarrow x=\dfrac{1}{104876}\)
Vậy GTLN P là 37/36 khi x = 1/104876
N
Giải chi tiết giúp mình nhé
3
NT
27 tháng 8 2021
d. \(\dfrac{x-2}{x-1}=\dfrac{x+4}{x+7}\)
\(\Rightarrow\left(x-2\right)\left(x+7\right)=\left(x-1\right)\left(x+4\right)\)
\(\Rightarrow x^2+5x-14=x^2+3x-4\)
\(\Rightarrow x^2+5x-x^2-3x=-4+14\)
\(\Rightarrow2x=10\) \(\Rightarrow x=\dfrac{10}{3}\) \(\Rightarrow x=5\)
KK
27 tháng 8 2021
\(\dfrac{x-2}{x-1}=\dfrac{x+4}{x+7}\)
⇔ \(\dfrac{\left(x-2\right)\left(x+7\right)}{\left(x-1\right)\left(x+7\right)}=\dfrac{\left(x+4\right)\left(x-1\right)}{\left(x+7\right)\left(x-1\right)}\)
⇔ (x - 2)(x + 7) = (x + 4)(x - 1)
⇔ x2 + 7x - 2x - 14 = x2 - x + 4x - 4
⇔ x2 - x2 + 7x - 2x + x - 4x = 14 - 4
⇔ 2x = 10
⇔ x = 10/2 = 5
13 tháng 7 2021
\(\dfrac{\sqrt{3}-3}{\sqrt{3}+1}=\dfrac{\left(\sqrt{3}-3\right)\left(\sqrt{3}-1\right)}{2}=\dfrac{3-\sqrt{3}-3\sqrt{3}+3}{2}=\dfrac{6-4\sqrt{3}}{2}=3-2\sqrt{3}\)
29 tháng 11 2021
\(x-114=113\\ x=113+114\\ x=227\)
\(3^2-3x=6^6.6^5\\ 9-3x=6^1=9-3x=6\\ 3x=9-6\\ 3x=3\\ x=1\)
23 tháng 1 2022
a) Có 15 học sinh đến trường bằng xe đạp.
b) Lớp 6A có 42 học sinh.
23 tháng 1 2022
a Có 15 học sinh đến trường bằng xe đạp
b Lớp 6A có 42 học sinh
d 40%
30 tháng 6 2023
3:
Gọi độ dài CD là x
Vận tốc người 1 là x/2
Vận tốc người 2 là x/3
Theo đề, ta có: 2/3(x/2-x/3)=20
=>x/2-x/3=30
=>x/6=30
=>x=180
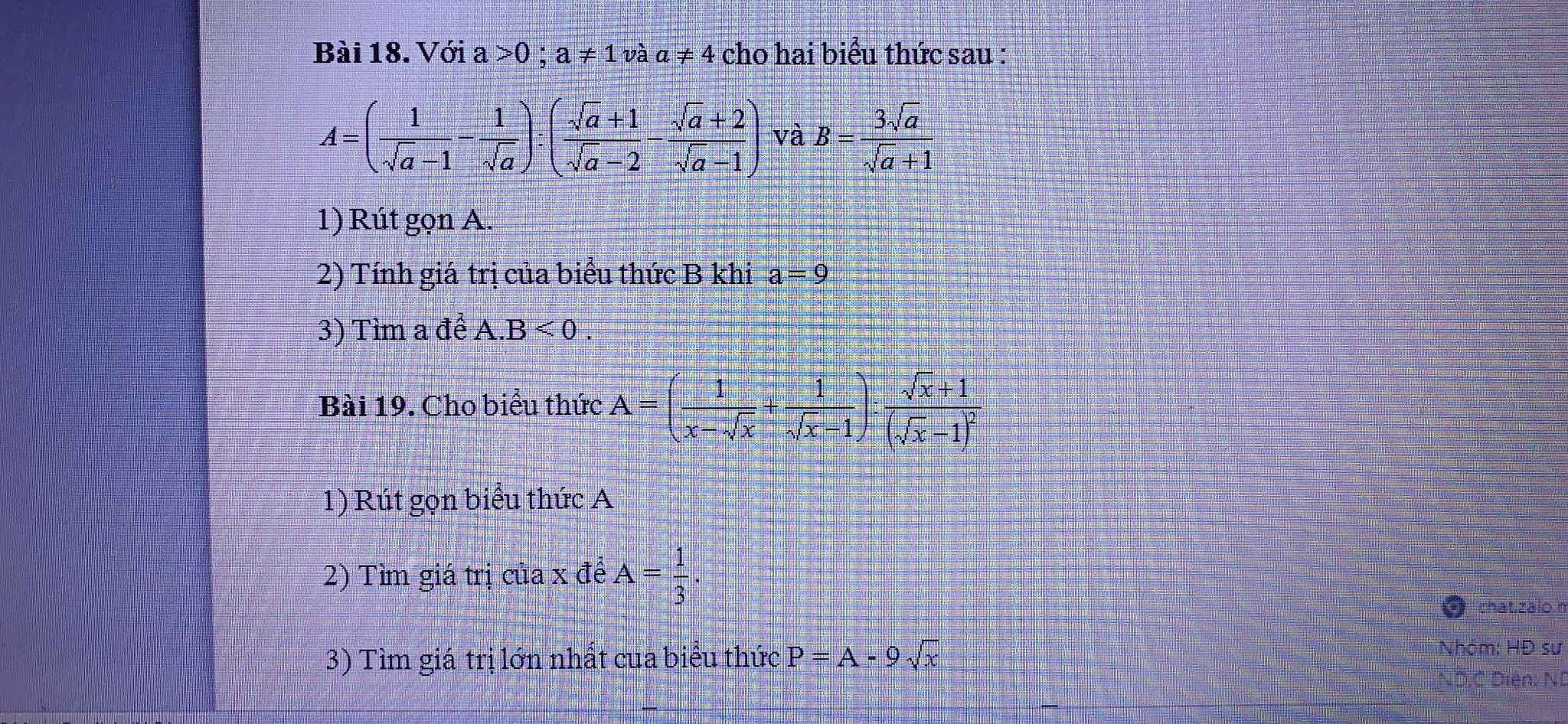
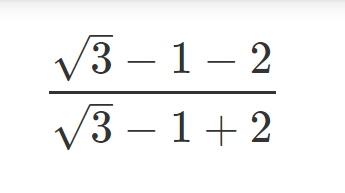
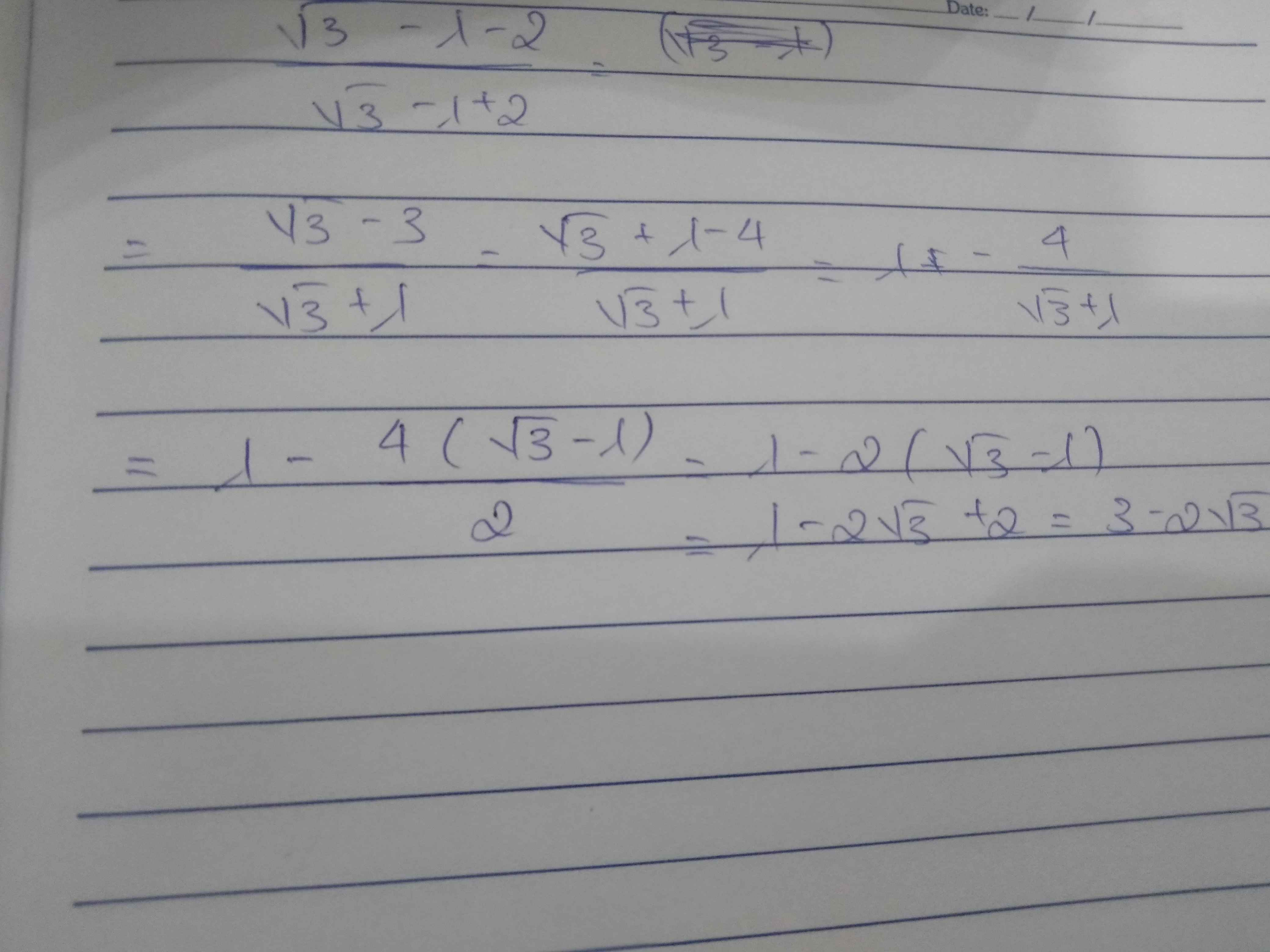
\(\left\{{}\begin{matrix}\dfrac{9}{\sqrt{2x-1}}+\dfrac{3}{y+1}=2\\\dfrac{4}{\sqrt{2x-1}}-\dfrac{1}{y+1}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{9}{\sqrt{2x-1}}+\dfrac{3}{y+1}=2\left(1\right)\\\dfrac{12}{\sqrt{2x-1}}-\dfrac{3}{y+1}=3\left(2\right)\end{matrix}\right.\)
Lấy \(\left(2\right)+\left(1\right)\) ta được:
\(\dfrac{21}{\sqrt{2x-1}}=5\\ \Leftrightarrow5\sqrt{2x-1}=21\\ \Leftrightarrow25\left(2x-1\right)=441\\ \Leftrightarrow50x-25=441\\ \Leftrightarrow50x=466\Leftrightarrow x=\dfrac{233}{25}\)
Thay x vào (1)
\(\dfrac{9}{\sqrt{2\cdot\dfrac{233}{25}-1}}+\dfrac{3}{y+1}=2\\ \Leftrightarrow\dfrac{9}{\sqrt{\dfrac{441}{25}}}+\dfrac{3}{y+1}=2\\ \Leftrightarrow\dfrac{9}{\dfrac{21}{5}}+\dfrac{3}{y+1}=2\\ \Leftrightarrow\dfrac{15}{7}+\dfrac{3}{y+1}=2\\ \Leftrightarrow15\left(y+1\right)+21=14\left(y+1\right)\\ \Leftrightarrow15y+15+21=14y+14\\ \Leftrightarrow y=-22\)
Vậy pt có tập nghiệm \(\left(x;y\right)=\left(\dfrac{233}{25};-22\right)\)
\(\left\{{}\begin{matrix}\dfrac{9}{\sqrt{2x-1}}+\dfrac{3}{y+1}=2\\\dfrac{4}{\sqrt{2x-1}}-\dfrac{1}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{36}{\sqrt{2x-1}}+\dfrac{12}{y+1}=8\\\dfrac{36}{\sqrt{2x-1}}-\dfrac{9}{y+1}=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{21}{y+1}=-1\\\dfrac{4}{\sqrt{2x-1}}-\dfrac{1}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y+1=-21\\\dfrac{4}{\sqrt{2x-1}}=\dfrac{20}{21}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-22\\2x-1=\dfrac{441}{25}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{233}{25}\\y=-22\end{matrix}\right.\)