Hãy chứng minh công thức tính điện trở tương đương Rtđ của đoạn mạch gồm hai điện trở R1, R2 mắc nối tiếp là: Rtđ = R1 + R2.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
25 tháng 8 2017
Hiệu điện thế giữa hai đầu đoạn mạch gồm hai điện trở mắc nối tiếp bằng tổng hai hiệu điện thế giữa hai đầu mỗi điện trở thành phần: U = U1 + U2
Ta có: U = U1+ U2 = I1.R1 + I2.R2 = I.(R1 + R2) (vì I = I1 = I2, tính chất đoạn mạch mắc nối tiếp)
Mà U = I.Rtđ → I.(R1 + R2) = I.Rtđ
Chia hai vế cho I ta được Rtđ = R1 + R2 (đpcm).
VT
17 tháng 4 2019
R t đ của đoạn mạch AB khi R 1 mắc nối tiếp với R 2 là: R t đ = R 1 + R 2 = 20 + 20 = 40Ω.
Vậy R t đ lớn hơn, mỗi điện trở thành phần.
31 tháng 10 2023
\(R_1ntR_2\)
Ta có : \(R_{tđ}=R_1+R_2\rightarrow R_2=R_{tđ}-R_1=9-3=6\left(\Omega\right)\)
NT
8 tháng 12 2016
A..Rtd1=20+40=60
B,,I=U/Rtd=0,1(A) U2=0,1x40=4
c,,,Rtd=Rtd1xR3)/(Rtd1+R3)=30
17 tháng 8 2021
a, \(Rtd=4\left(om\right)< R1=6\left(om\right)\)
=>cần mắc 2 điện trở nối tiếp R1//R2
\(=>4=\dfrac{6R2}{6+R2}=>R2=12\left(om\right)\)
b,\(Rtd=9\left(om\right)>R1=>R1ntR2\)
\(=>9=R1+R2=>R2=3\left(om\right)\)
TV
3
J
16 tháng 10 2021
tóm tắc
\(R_1=R_2=6\left(\text{ Ω}\right)\)
\(R_{tđ}=?\)
Giải
Điện trở tương đương của đoạn mạch là:
\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}\Rightarrow R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{6.6}{6+6}=3\left(\text{Ω}\right)\)
Đáp số : \(R_{tđ}=3\text{Ω}\)
VT
28 tháng 1 2017
Công thức tính điện trở tương đương đối với:
Đoạn mạch gồm hai điện trở R1 và R2 mắc nối tiếp: Rtđ = R1 + R2
Đoạn mạch gồm hai điện trở R1 và R2 mắc song song.
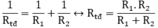
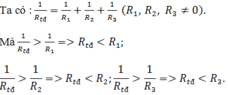
Trong mạch nối tiếp, ta có:
U = U1 + U2 = IR1 + IR2 = I(R1 + R2).
Mặt khác, U = IRtđ. Từ đó suy ra: Rtđ = R1 + R2.
Ta có:U=U1+U2=IR1+IR2=I.(R1+R2)
mà U=IRtđ
Suyra Rtđ=R1+R2