Tìm tập hợp các điểm cách đều hai đường thẳng :
\(\Delta_1:5x+3y-3=0\)
\(\Delta_2:5x+3y+7=0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DM
Đức Minh
30 tháng 3 2017
Đúng(0)
TG
Trà Giang
30 tháng 3 2017
Đúng(0)
Những câu hỏi liên quan
10 tháng 4 2017
lời giải
\(\Delta_1\) //\(\Delta_2\)
Vậy \(\Delta_3\) cách đều phải //\(\Delta_2\) và \(\Delta_1\) và giữa \(\Delta_1\&\Delta_2\)
M(0,b)
x=0 =>\(\left\{{}\begin{matrix}\Delta_1=y=1\\\Delta_2\Rightarrow y=-\dfrac{7}{3}\end{matrix}\right.\)
=> b=\(\dfrac{\dfrac{3}{3}-\dfrac{7}{3}}{2}=\dfrac{-2}{3}\)
\(M=\left(0,-\dfrac{2}{3}\right)\)
\(\Delta_3\) phải đi qua M
=>\(\Delta_3\)=5x+3(y+2/3)=5x+3y+2=0
Đáp số: \(\Delta_3\)=5x+3y+2=0
PT
1
CM
3 tháng 12 2018
Gọi điểm cách đều hai đường thẳng (Δ1) và (Δ2) là M(x, y).
Ta có:
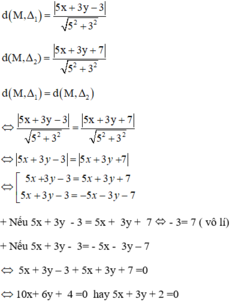
Vậy tập hợp các điểm M cách đều hai đường thẳng đã cho là đường thẳng: 5x + 3y + 2 = 0.
30 tháng 6 2023
a: Tọa độ A là:
4x-3y-12=0 và 4x+3y-13=0
=>A(25/8;1/6)
Tọa độ B là:
x=0 và 4x-3y-12=0
=>x=0 và y=-4
Tọa độ C là:
x=0 và 4x+3y-13=0
=>y=13/3
b: A(25/8;1/6); B(0;-4); C(0;13/3)
\(AB=\sqrt{\left(0-\dfrac{25}{8}\right)^2+\left(-4-\dfrac{1}{6}\right)^2}=\dfrac{125}{24}\left(cm\right)\)
\(AC=\sqrt{\left(0-\dfrac{25}{8}\right)^2+\left(\dfrac{13}{3}-\dfrac{1}{6}\right)^2}=\dfrac{125}{24}\left(cm\right)\)
\(BC=\sqrt{0^2+\left(\dfrac{13}{3}+4\right)^2}=\dfrac{25}{3}\)
\(P=\dfrac{1}{2}\left(\dfrac{125}{24}+\dfrac{125}{24}+\dfrac{25}{3}\right)=\dfrac{75}{8}\)
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{-7}{25}\)
=>sin A=24/25
\(S_{ABC}=\dfrac{1}{2}\cdot\dfrac{24}{25}\cdot\dfrac{125}{24}\cdot\dfrac{125}{24}=\dfrac{625}{48}\)
=>r=625/48:75/8=25/18
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 5 2020
Gọi \(M\left(x;y\right)\) là điểm thuộc phân giác của 2 đường thẳng
\(\Leftrightarrow d\left(M;\Delta_1\right)=d\left(M;\Delta_2\right)\)
a/ \(\frac{\left|2x+4y+7\right|}{\sqrt{2^2+4^2}}=\frac{\left|5x+3y+7\right|}{\sqrt{5^2+3^2}}\)
\(\Leftrightarrow\sqrt{17}\left|2x+4y+7\right|=\sqrt{10}\left|5x+3y+7\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2\sqrt{17}x+4\sqrt{17}y+7\sqrt{17}=5\sqrt{10}x+3\sqrt{10}y+7\sqrt{10}\\2\sqrt{17}x+4\sqrt{17}y+7\sqrt{17}=-5\sqrt{10}x-3\sqrt{10}y-7\sqrt{10}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(2\sqrt{17}-5\sqrt{10}\right)x+\left(4\sqrt{17}-3\sqrt{10}\right)y+7\sqrt{17}-7\sqrt{10}=0\\\left(2\sqrt{17}+5\sqrt{10}\right)x+\left(4\sqrt{17}+3\sqrt{10}\right)y+7\sqrt{17}+7\sqrt{10}=0\end{matrix}\right.\)
Câu b bạn làm tương tự. Số xấu quá nhìn chẳng muốn làm luôn
31 tháng 5 2020
hình như bạn nhầm \(\sqrt{5^2+3^2}=\sqrt{34}\) chứ sai lại là \(\sqrt{17}\)
CM
23 tháng 7 2017
Quỹ tích các điểm cách đều hai đường thẳng d1: 5x-12y+4=0, d2: 4x-3y+2=0 là hai đường phân giác ∆1,2 của chúng
Phương trình ∆1 là
5 x − 12 y + 4 5 2 + ( − 12 ) 2 = 4 x − 3 y + 2 4 2 + ( − 3 ) 2 ⇔ 5 x − 12 y + 4 13 = 4 x − 3 y + 2 5 ⇔ 5 ( 5 x − 12 y + 4 ) = 13 ( 4 x − 3 y + 2 ) ⇔ 25 x − 60 y + 20 = 52 x − 39 y + 26 ⇔ − 27 x − 21 y − 6 = 0 ⇔ 9 x + 7 y + 2 = 0
Phương trình ∆2 là
5 x − 12 y + 4 5 2 + ( − 12 ) 2 = − 4 x − 3 y + 2 4 2 + ( − 3 ) 2 ⇔ 5 x − 12 y + 4 13 = − 4 x − 3 y + 2 5 ⇔ 5 ( 5 x − 12 y + 4 ) = − 13 ( 4 x − 3 y + 2 ) ⇔ 25 x − 60 y + 20 = − 52 x + 39 y − 26 ⇔ 77 x − 99 y + 46 = 0
Đáp án D
20 tháng 2 2021
Gọi \(M\left(x;y\right)\)
\(d\left(M,d\right)=\dfrac{5}{13}d\left(M,\Delta\right)\Leftrightarrow\dfrac{\left|5x-12y+4\right|}{13}=\dfrac{5}{13}.\dfrac{\left|4x-3y-10\right|}{5}\Leftrightarrow\left[{}\begin{matrix}x-9y+14=0\\9x-15y-6=0\end{matrix}\right.\)
1 tháng 4 2016
Đường thẳng \(\Delta_1\) có vec tơ pháp tuyến \(\overrightarrow{n_1}=\left(3;4\right)\)
Đường thẳng \(\Delta_2\) có vec tơ pháp tuyến \(\overrightarrow{n_2}=\left(4;-3\right)\)
Do \(\overrightarrow{n_1}.\overrightarrow{n_2}=3.4+4.\left(-3\right)=0\) nên \(\Delta_1\perp\Delta_2\)
Do đó nếu đường thẳng d tạo với \(\Delta_1,\Delta_2\) một tam giác cân, thì đó là tam giác vuông cân, tại đỉnh là giao điểm của \(\Delta_1;\Delta_2\)
Bài toán quy về viết phương trình đường thẳng d đi qua điểm M(1;1) và tạo với đường thẳng \(\Delta_1\) một góc \(\frac{\pi}{4}\).
Giả sử đường thẳng d có vec tơ pháp tuyến \(\overrightarrow{m}=\left(a;b\right)\) với \(a^2+b^2\ne0\), khi đó d có phương trình dạng :
\(ax+by-a-b=0\)
Do góc \(\left(d;\Delta_1\right)=\frac{\pi}{4}\) nên
\(\frac{\left|3a+4b\right|}{5\sqrt{a^2+b^2}}=\frac{1}{\sqrt{2}}\Leftrightarrow7a^2-48ab-7b^2=0\)
\(\Leftrightarrow\begin{cases}a=7b\\7a=-b\end{cases}\)
Nếu a=7b, chọn b=1, a=7, ta được đường thẳng d : \(7x+y-8=0\)
Nếu 7a=-b, chọn a=1, b=-7 ta được đường thẳng d : \(x-7y+6=0\)