Từ hệ thức \(a^2=b^2+c^2-2bc\cos A\) trong tam giác, hãy suy ra định lý Pi-ta-go ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giả sử tam giác ABC vuông tại A, suy ra góc A = 90º, đặt BC = a, CA = b, AB = c
Theo định lý Cô sin trong tam giác ta có:
a2 = b2 + c2 – 2bc.cos A = b2 + c2 – 2bc.cos 90º = b2 + c2 – 2bc.0 = b2 + c2 .
Vậy trong tam giác ABC vuông tại A thì a2 = b2 + c2 (Định lý Pytago).

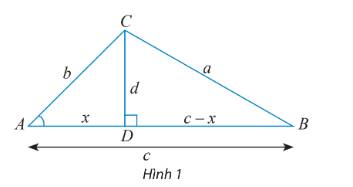
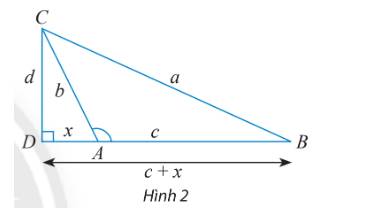
a) ? = x vì \(\cos A = \frac{{AD}}{{AC}} = \frac{x}{b} \Rightarrow ? = x.\)
b) Xét tam giác vuông BCD, ta có: \({a^2} = {d^2} + {(c + x)^2} = {d^2} + {x^2} + {c^2} + 2xc\) (1)
Xét tam giác vuông ACD, ta có: \({b^2} = {d^2} + {x^2} \Rightarrow {d^2} = {b^2} - {x^2}\) (2)
\(\cos A = - \cos \widehat {DAC} = - \frac{x}{b} \Rightarrow x = - b\cos A.\) (3)
Thay (2) và (3) vào (1), ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
c) Ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Mà \(\widehat A = {90^o} \Rightarrow \cos A = \cos {90^o} = 0.\)
\( \Rightarrow {a^2} = {b^2} + {c^2}\)

Ta có: \(S_{\Delta ABC}=\frac{1}{2}AB.AC=\frac{1}{2}BC.AH\)
\(\Rightarrow\frac{1}{AB.AC}=\frac{1}{BC.AH}\)
\(\Rightarrow\frac{1}{AH}=\frac{BC}{AB.AC}\)
\(\Rightarrow\frac{1}{AH^2}=\frac{BC^2}{AB^2.AC^2}=\frac{AB^2+AC^2}{AB^2.AC^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)

kẻ BH _|_ BC tại H
xét tam giác ABH vuông tại H
=> góc ABH + góc BAC = 90 (đl)
góc BAC = 60 (gt)
=> góc ABH = 30 ; xét tam giác ABH vuông tại H
=> AH = BA/2 (định lí)
=> AB = 2AH (1)
xét tam giác ABH vuông tại H
=> AB^2 = AH^2 + BH^2 (đl pytago)
=> BH^2 = AB^2 - AH^2 (2)
xét tam giác BHC vuông tại H
=> BC^2 = HC^2 + BH^2 (đl Pytago)
HC = AC - AH
=> BC^2 = (AC - AH)^2 + BH^2
=> BC^2 = AC^2 - 2AC.AH + AH^2 + BH^2 và (1)(2)
=> BC^2 = AC^2 - AB.AC + AH^2 + AB^2 - AH^2
=> BC^2 = AB^2 + AC^2 - AB.AC


Định lí cosin: Trong tam giác ABC
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\quad (1)\\{b^2} = {a^2} + {c^2} - \,2a\,c.\cos B\quad (2)\\{c^2} = {b^2} + {a^2} - \,2ab.\cos C\quad (3)\end{array}\)
Ta có \((1) \Leftrightarrow 2bc\cos A = {b^2} + {c^2} - {a^2}\, \Leftrightarrow \cos A = \frac{{{b^2} + {c^2} - {a^2}\,}}{{2b\,c}}.\)
Tương tự từ (2) và (3) ta suy ra \(\cos B = \frac{{{a^2} + {c^2} - {b^2}\,}}{{2a\,c}}\); \(\cos C = \frac{{{b^2} + {a^2} - {c^2}\,}}{{2b\,a}}\)

Áp dụng định lí Pytago ta có
\(BC^2=AB^2+AC^2\\ =\sqrt{6^2+8^2}=10\)
góc A =90o => cosA = 0
nên a2 = b2 +c2
Định lí Pi ta go là:
Kết hợp cả định lý thuận và đảo, có thể viết định lý Pythagoras dưới dạng: Một tam giác có ba cạnh a, b và c, thì nó là tam giác vuông với góc vuông giữa a và b khi và chỉ khi a2 + b2 = c.