Với a , b > 0 chứng minh \(\dfrac{a+b}{2}\ge\sqrt{ab}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 5 2018
\(bdt\Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\) (đúng) . Dấu "=" khi a=b
21 tháng 5 2018
Xét \(a+b\ge2\sqrt{ab}\)
\(\Leftrightarrow a+b-2\sqrt{ab}\ge0\)
\(\Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\) (luôn đúng với mọi a, b)
\(\Leftrightarrow\) đpcm
ND
3 tháng 5 2018
e)
\(\dfrac{a^2+b^2+c^2}{3}\ge\left(\dfrac{a+b+c}{3}\right)^2\)
\(\Leftrightarrow3\left(a^2+b^2+c^2\right)\ge a^2+b^2+c^2+2\left(ab+bc+ca\right)\)
\(\Leftrightarrow2\left(a^2+b^2+c^2\right)\ge2\left(ab+bc+ac\right)\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2ac-2bc\ge0\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(a^2-2ac+c^2\right)+\left(b^2-2bc+c^2\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(a-c\right)^2+\left(b-c\right)^2\ge0\) ( luôn đúng)
=> ĐPCM
15 tháng 4 2021
a, \(\sqrt{\frac{2a}{3}}.\sqrt{\frac{3a}{8}}=\sqrt{\frac{6a^2}{24}}=\sqrt{\frac{a^2}{4}}=\left|\frac{a}{2}\right|=\frac{a}{2}\)
do \(a\ge0\)
b, \(\sqrt{13a}.\sqrt{\frac{52}{a}}=\sqrt{\frac{676a}{a}}=\sqrt{676}=26\)
c, \(\sqrt{5a}.\sqrt{45a}-3a=\sqrt{225a^2}-3a=\left|15a\right|-3a\)
\(=15a-3a=12a\)do a > 0
d, \(=\left(3-a\right)^2-\sqrt{0,2}.\sqrt{180a^2}\)
\(=\left(3-a\right)^2-\sqrt{36a^2}=\left(3-a\right)^2-\left|6a\right|\)
Với \(a\ge0\Rightarrow\left(3-a\right)^2-6a=a^2-6a+9-6a=a^2-12a+9\)
Với \(a< 0\Rightarrow\left(3-a\right)^2+6a=a^2-6a+9+6a=a^2+9\)
UK
13 tháng 8 2017
Đặt b+c=x;c+a=y;a+b=z
Áp dụng BĐT \(\left(x+y+z\right)\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)\ge9\), ta được
\(2\left(a+b+c\right)\left(\dfrac{1}{b+c}+\dfrac{1}{a+c}+\dfrac{1}{a+b}\right)\ge9\)
\(\left(a+b+c\right)\left(\dfrac{1}{b+c}+\dfrac{1}{a+c}+\dfrac{1}{a+b}\right)\ge4,5\)
\(\)\(\dfrac{a+b+c}{b+c}+\dfrac{a+b+c}{a+c}+\dfrac{a+b+c}{a+b}\ge4,5\)
\(\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}+1+1+1\ge4,5\)
\(\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}\ge1,5\)
Đẳng thức xảy ra khi và chỉ khi a=b=c
TN
26 tháng 7 2018
Ta có :VP= \(\dfrac{1}{\left|B\right|}.\sqrt{A}.\sqrt{B}=\dfrac{\sqrt{A}.\sqrt{B}}{B}\)(vì B > 0)
\(=\dfrac{\sqrt{A}.\sqrt{B}}{\sqrt{B}.\sqrt{B}}=\dfrac{\sqrt{A}}{\sqrt{B}}=\sqrt{\dfrac{A}{B}}=VT\)(đpcm)
26 tháng 7 2018
\(vp=\dfrac{1}{\left|B\right|}.\sqrt{AB}=\dfrac{\sqrt{A}.\sqrt{B}}{B}=\dfrac{\sqrt{A}}{\sqrt{B}}=\sqrt{\dfrac{A}{B}}=vt\)
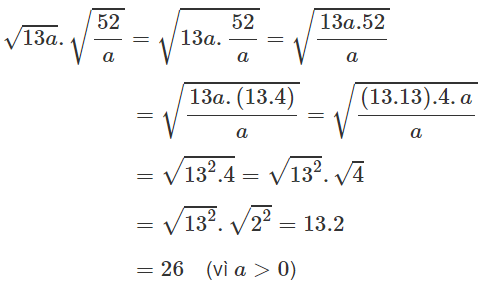
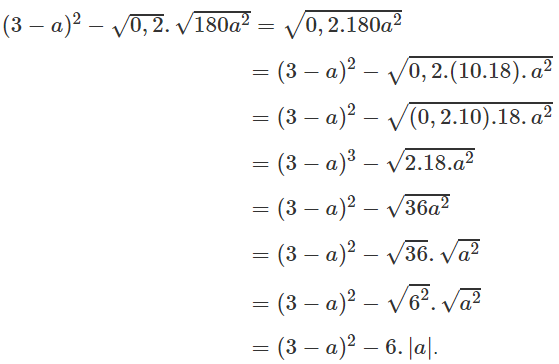
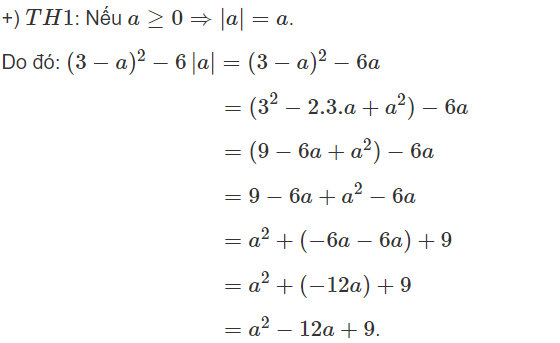
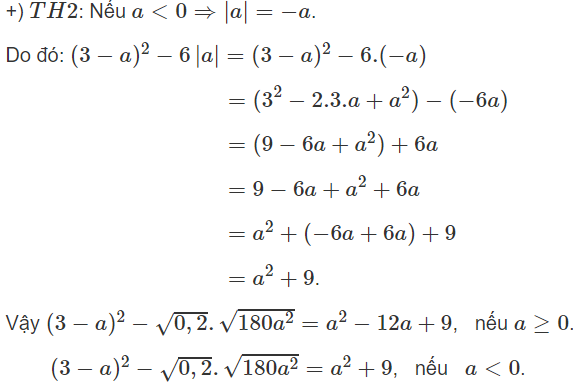
bất đẳng thức cô-si ?
\(\dfrac{a+b}{2}\ge\sqrt{ab}\\ < =>a+b\ge2\sqrt{ab}\\ < =>\left(a+b\right)^2\ge4ab\\ < =>a^2+2ab+b^2\ge4ab\\ < =>a^2-2ab+b^2\ge0\\ < =>\left(a-b\right)^2\ge0\left(đúng\right)\)
=> \(\dfrac{a+b}{2}\ge\sqrt{ab}\)
chúc may mắn
Ta có: \(a\ge0;b\ge0\Rightarrow a+b\ge0\Leftrightarrow a^2+2ab+b^2\ge2ab\)
\(\Leftrightarrow\left(a+b\right)^2\ge2ab\Leftrightarrow a+b\ge\sqrt{2}.\sqrt{ab}\)
\(\Leftrightarrow2.\dfrac{a+b}{2}\ge\sqrt{2}.\sqrt{ab}\); do \(2>\sqrt{2}\) nên \(\dfrac{a+b}{2}\ge\sqrt{ab}\)