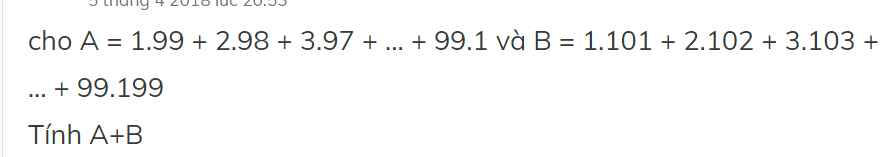B= 1.101 + 2.102 + 3.103 + ... + 99.199
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
IA
5 tháng 4 2018
A+B = (1.99+2.98+3.97+...+99.1)+(1.101+2.102+3.103+...+99.199)
A+B = (1.99+1.101)+(2.98+2.102)+(3.97+3.103)+...+(99.1+99.199)
A+B = 1(99+101) + 2(98+102) + 3(97.103)+...+99(1+199)
A+B = 1.200 + 2.200 + 3.200 +...+ 99.200
A+B = 200.(1+2+3+...+200)
A+B = 200.4950
A+B = 990000
HD
1
20 tháng 4 2017
A + B = ( 1 . 99 + 2 . 98 + 3 . 97 + ... + 99 . 1 ) + ( 1 . 101 + 2 . 102 + 3 . 103 + ... + 99 . 199 )
A + B = 99 . ( 1 + 199 ) + 98 . ( 2 + 198 ) + 97 . ( 3 + 197 ) + ... + 2 . ( 102 + 98 ) + 1 . ( 99 + 101 )
A + B = 99 . 200 + 98 . 200 + 97 . 200 + ... + 2 . 200 + 1 . 200
A + B = ( 99 + 98 + 97 + ... + 2 + 1 ) . 200
A + B = 4950 . 200
A + B = 990000
5 tháng 4 2017
A+B=(1.99+2.98+...+99.1)+(1.101+2.102+...+99.199)
=(1.99+1.101)+(2.98+2.102)+...+(99.1+99.199)
=1.(99+101)+2.(98+102)+...+99(1+199)
=200+2.200+...+99.200
=200.(1+2+3+4+...+99)
=200.4950
=.....
NT
0
NT
0
NM
1
NA
1
5 tháng 3 2019
Ta có:
$(\frac{1}{1.101}+\frac{1}{2.102}+...+\frac{1}{10.110}).x=\frac{1}{1.11}+\frac{1}{2.12}+...+\frac{1}{100.110}$
$\Leftrightarrow \frac{1}{100}\left ( \frac{1}{1}-\frac{1}{100}+\frac{1}{2}-\frac{1}{102}+...+\frac{1}{10}-\frac{1}{110} \right )x=\frac{1}{10}\left ( \frac{1}{1}-\frac{1}{11}+\frac{1}{2}-\frac{1}{12}+...+\frac{1}{100}-\frac{1}{110} \right )$
$\Leftrightarrow \left ( \frac{1}{1}-\frac{1}{100}+\frac{1}{2}-\frac{1}{102}+...+\frac{1}{10}-\frac{1}{110} \right )x=10\left ( \frac{1}{1}-\frac{1}{11}+\frac{1}{2}-\frac{1}{12}+...+\frac{1}{100}-\frac{1}{110} \right )$
Đặt $A=\frac{1}{1}-\frac{1}{11}+\frac{1}{2}-\frac{1}{12}+...+\frac{1}{100}-\frac{1}{110}$
$\Rightarrow A=\left ( 1+\frac{1}{2}+...+\frac{1}{10} \right )+\left ( \frac{1}{11}+\frac{1}{12}+...+\frac{1}{100} \right )-\left ( \frac{1}{11}+\frac{1}{12}+...+\frac{1}{100} \right )-\left (\frac{1}{101}+\frac{1}{102}+...+\frac{1}{110} \right )$
$\Rightarrow A=\left ( 1+\frac{1}{2}+...+\frac{1}{10} \right )-\left (\frac{1}{101}+\frac{1}{102}+...+\frac{1}{110} \right )$
$\Rightarrow A=\frac{1}{1}-\frac{1}{100}+\frac{1}{2}-\frac{1}{102}+...+\frac{1}{10}-\frac{1}{110}$
Thay vào phương trình, ta có:
$\left ( \frac{1}{1}-\frac{1}{100}+\frac{1}{2}-\frac{1}{102}+...+\frac{1}{10}-\frac{1}{110} \right )x=10\left ( \frac{1}{1}-\frac{1}{100}+\frac{1}{2}-\frac{1}{102}+...+\frac{1}{10}-\frac{1}{110} \right )$
$\Leftrightarrow x=10$