Bài 6. Cho hai đường thẳng 
. Tìm m để góc giữa hai đường thẳng đó 
, với:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NM
1
Những câu hỏi liên quan
15 tháng 11 2021
Ghi lại đề: \(y=\left(m+1\right)x-3;y=\left(2m-1\right)x+4\)
\(a,m=-\dfrac{1}{2}\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{1}{2}x-3\\y=-2x+4\end{matrix}\right.\)
Hệ số a 2 đt đã cho là \(\dfrac{1}{2};-2\) có tích là -1 nên 2 đt vuông góc
\(b,\Leftrightarrow\left(m+1\right)\left(2m-1\right)=-1\\ \Leftrightarrow2m^2+m-1=-1\\ \Leftrightarrow2m^2+m=0\\ \Leftrightarrow m\left(2m-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=0\\m=\dfrac{1}{2}\end{matrix}\right.\)
17 tháng 11 2021
\(1,\Leftrightarrow\left\{{}\begin{matrix}a=-3\\4\ne-1\end{matrix}\right.\Leftrightarrow a=-3\\ 2,\Leftrightarrow\left\{{}\begin{matrix}2m=m-1\\1\ne3\end{matrix}\right.\left(m\ne0;m\ne1\right)\Leftrightarrow m=-1\\ 3,\)
PTHDGD: \(x+3=mx-1\)
Mà chúng cắt tại hoành độ 1 nên \(x=1\Leftrightarrow m-1=4\Leftrightarrow m=5\)
\(5,A\left(2;4\right)\inđths\Leftrightarrow2a+2=4\Leftrightarrow a=1\Leftrightarrow y=x+2\)
PT giao Ox: \(x+2=0\Leftrightarrow x=-2\Leftrightarrow A\left(-2;0\right)\Leftrightarrow OA=2\)
PT giao Oy: \(y=2\Leftrightarrow B\left(0;2\right)\Leftrightarrow OB=2\)
Vì \(OA=OB\) nên OAB vuông cân
Vậy góc tạo bởi đths là 450
2 tháng 10 2021
2 hàm số bậc nhất \(y=mx+3,y=\left(2m+1\right)x-5\left(đk:m\ne0,m\ne-\dfrac{1}{2}\right)\)
a) Để 2 đường thẳng song song với nhau thì:
\(\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\m=2m+1\\3\ne-5\left(luôn.đúng\right)\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\m=-1\end{matrix}\right.\)
b) Để 2 đường thẳng cắt nhau:
\(\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\m\ne2m+1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\m\ne-1\end{matrix}\right.\)
c) Để 2 đường thẳng vuông góc với nhau:
\(\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\m\left(2m+1\right)=-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\2m^2+m+1=0\left(VLý.do.2m^2+m+1=2\left(m+\dfrac{1}{4}\right)^2+\dfrac{7}{8}>0\right)\end{matrix}\right.\)
Vậy 2 đường thẳng này không vuông góc với nhau với mọi m
2 tháng 10 2021
\(a,\Leftrightarrow\left\{{}\begin{matrix}m=2m+1\\-5\ne3\end{matrix}\right.\Leftrightarrow m=-1\\ b,\Leftrightarrow m\ne2m+1\Leftrightarrow m\ne-1\\ c,\Leftrightarrow m\left(2m+1\right)=-1\\ \Leftrightarrow2m^2+m+1=0\\ \Delta=1-8< 0\\ \Leftrightarrow m\in\varnothing\)
Vậy 2 đt không thể vuông góc nhau
4 tháng 3 2021
Câu 1:
Ta có: \(ax+\left(2a-1\right)y+3=0\)
\(\Leftrightarrow\left(2a-1\right)y=-ax-3\)
\(\Leftrightarrow y=\dfrac{-ax-3}{2a-1}\)
Để (d) đi qua điểm M(1;-1) thì
Thay x=1 và y=-1 vào hàm số \(y=\dfrac{-ax-3}{2a-1}\), ta được:
\(\dfrac{-a\cdot1-3}{2a-1}=-1\)
\(\Leftrightarrow-a-3=-1\left(2a-1\right)\)
\(\Leftrightarrow-a-3=-2a+1\)
\(\Leftrightarrow-a+2a=1+3\)
hay a=4
Vậy: a=4
và hệ số góc của (d) là 4
QT
Quoc Tran Anh Le
Giáo viên
24 tháng 8 2023
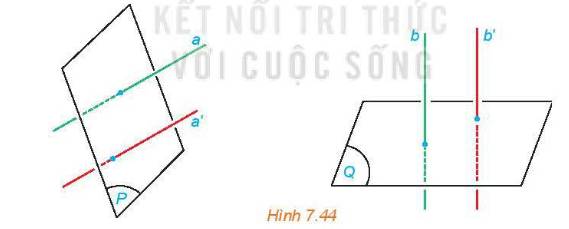
Vì hai đường thẳng a, a' cùng vuông góc với (P), hai đường thẳng b, b' cùng vuông góc với (Q) nên a // a', b // b'
Vậy (a,b) = (a', b')
Lời giải:
Áp dụng công thức tính góc giữa hai đường thẳng thôi:
\(\cos (d,\Delta)=\frac{|(m+3)(m-2)-(m-1)(m+1)|}{\sqrt{(m+3)^2+(m-1)^2}\sqrt{(m-2)^2+(m+1)^2}}=\cos 90=0\)
\(\Leftrightarrow (m+3)(m-2)-(m-1)(m+1)=0\)
\(\Leftrightarrow m-5=0\Leftrightarrow m=5\)
Vậy $m=5$