Cho hai điểm A(0;0;3) và B(1;-2;-3). Gọi A'B' là hình chiếu vuông góc của đường thẳng AB lên mặt phẳng (Oxy). Viết phương trình tham số của đường thẳng A'B'.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 1 2019
Do đó I(1; 3; 4)
Phương trình mặt phẳng ( α ) qua I và vuông góc với OA là: x – 1 = 0, ( α ) cắt OA tại K(1; 0; 0)
Khoảng cách từ I đến OA là:
CM
14 tháng 11 2017
Chọn A
Gọi phương trình mặt phẳng là
Theo đề bài, mặt phẳng qua A, B nên ta có:
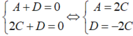
Vậy mặt phẳng (P) có dạng: 2Cx + 2By + Cz - 2C = 0. (S) có tâm I (1; 1; 0) và R = 1
Vì (P) tiếp xúc với (S) nên d(I, (P)) = R
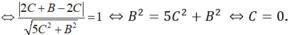
Suy ra A = D = 0. Vậy phương trình mặt phẳng (P): y = 0
CM
21 tháng 4 2018
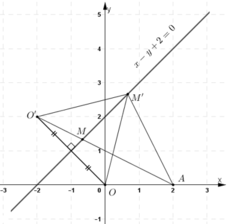
a, Cách 1: Gọi O’ là điểm đối xứng với O qua (Δ)
⇒ OO’ ⊥ Δ tại trung điểm I của OO’.
+ (Δ) nhận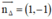 
là một vtpt ⇒ (Δ) nhận 
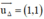là một vtcp
OO’ ⊥ Δ ⇒ OO’ nhận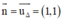 
là một vtpt. Mà O(0, 0) ∈ OO’
⇒ Phương trình đường thẳng OO’: x + y = 0.
+ I là giao OO’ và Δ nên tọa độ của I là nghiệm của hệ phương trình:
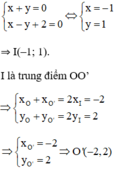
Cách 2: Gọi O’(x, y) là điểm đối xứng với O qua Δ.
+ Trung điểm I của OO’ là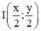 
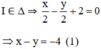
+ (Δ) nhận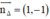 
là một vtpt ⇒ (Δ) nhận 
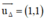là một vtcp.
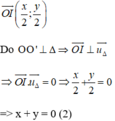
Từ (1) và (2) ta có hệ phương trình
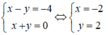
Vậy O’(–2; 2).
b)
+ Vì O và A nằm cùng một nửa mặt phẳng bờ là đường thẳng Δ nên đoạn thẳng OA không cắt Δ.
O’ và A thuộc hai nửa mặt phẳng khác nhau bờ là đường thẳng Δ nên O’A cắt Δ.
Do O’ đối xứng với O qua đường thẳng ∆ nên ∆ là đường trung trực của đoạn thẳng OO’, với mọi M ∈ Δ ta có MO = MO’.
Độ dài đường gấp khúc OMA bằng OM + MA = O’M + MA ≥ O’A.
⇒ O’M + MA ngắn nhất khi O’M + MA = O’A ⇔ M là giao điểm của O’A và Δ.
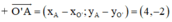
⇒ O’A nhận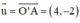 
là một vtcp
⇒ O’A nhận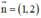 
là một vtpt. Mà A(2; 0) ∈ O’A
⇒ Phương trình đường thẳng O’A : 1(x - 2) + 2(y - 0)= 0 hay x + 2y – 2 = 0.
M là giao điểm của O’A và Δ nên tọa độ điểm M là nghiệm của hệ :
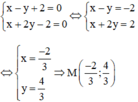
Vậy điểm M cần tìm là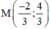 
HP
9 tháng 5 2021
Trước hết ta thấy O, A nằm trên cùng một mặt phẳng bờ \(\Delta\).
Qua A kẻ đường thẳng d vuông góc với \(\Delta\) tại H.
Đường thẳng d có phương trình: \(x+y-2=0\)
\(\Rightarrow H\) có tọa độ là nghiệm hệ \(\left\{{}\begin{matrix}x-y+2=0\\x+y-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\Rightarrow H=\left(0;2\right)\)
Gọi A' là điểm đối xứng với A qua d
\(\Rightarrow\left\{{}\begin{matrix}x_{A'}=2x_H-x_A=-2\\y_{A'}=2y_H-y_A=4\end{matrix}\right.\Rightarrow A'=\left(-2;4\right)\)
\(\Rightarrow OA'=2\sqrt{5}\)
Phương trình đường thẳng OA': \(2x+y=0\)
Khi đó: \(OM+MA=OM+MA'\ge OA'=2\sqrt{5}\)
\(min=2\sqrt{5}\Leftrightarrow M\) là giao điểm của \(\Delta\) và OA'
\(\Leftrightarrow M\) có tọa độ là nghiệm hệ \(\left\{{}\begin{matrix}x-y+2=0\\2x+y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{2}{3}\\y=\dfrac{4}{3}\end{matrix}\right.\Rightarrow M=\left(-\dfrac{2}{3};\dfrac{4}{3}\right)\)
AH
Akai Haruma
Giáo viên
9 tháng 5 2021
Lời giải:
Vì $M$ thuộc $\Delta$ nên $M$ có tọa độ $(a-2,a)$
Độ dài đường gấp khúc $OMA$ là:
$OM+MA=\sqrt{a^2+(a-2)^2}+\sqrt{(a-4)^2+a^2}$
$=\sqrt{2}.(\sqrt{(a-1)^2+1}+\sqrt{(2-a)^2+2^2})$
$\geq \sqrt{2}.\sqrt{(a-1+2-a)^2+(1+2)^2}$ (theo BĐT Mincopxky)
$=2\sqrt{5}$
Vậy $OMA$ min bằng $2\sqrt{5}$. Giá trị này đạt tại $a=\frac{4}{3}$
Vậy $M(\frac{-2}{3},\frac{4}{3})$
CM
19 tháng 2 2018
Đáp án D
Ta có f = 3 x - y + z - 2 ⇒ f A . f B = 1 . 8 = 8 > 0 ⇒ A, B nằm về hai phía đối với α .
PT
1
CM
23 tháng 10 2017
Ta có: AB → = (−1; −2; 1)
AC → = (−1; −3; 0)
Ba điểm A, B, C thẳng hàng khi và chỉ khi hai vecto AB → và AC → cùng phương, nghĩa là AB → = k AC → với k là một số thực.
Giả sử ta có AB → = k AC →
khi đó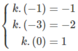 
Ta không tìm được số k nào thỏa mãn đồng thời cả ba đẳng thức trên. Vậy ba điểm A, B, C không thẳng hàng.
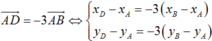
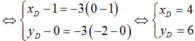
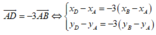
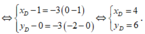
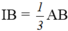
Giải:
Gọi \((l)\) là mặt phẳng chứa đường thẳng đi qua $AB$ và vuông góc với mặt phẳng $(Oxy)$
\(\overrightarrow{n_l}=[\overrightarrow{AB},\overrightarrow{n_{Oxy}}]=[\overrightarrow{AB},\overrightarrow{Oz}]=(2,1,0)\)
Suy ra PTMP $(l)$ là : \(2x+y=0\)
Ta thấy \(A'B'=(Oxy)\cap (l)\)
\(\Rightarrow \overrightarrow{u_{A'B'}}=[\overrightarrow{n_{Oxy}},\overrightarrow{n_l}]=(1,-2,0)\)
Mặt khác điểm \((1,-2,0)\) thuộc đường thẳng $A'B'$
\(\Rightarrow \) PTĐT: \(\left\{{}\begin{matrix}x=t+1\\y=-2-2t\\z=0\end{matrix}\right.\)