
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()

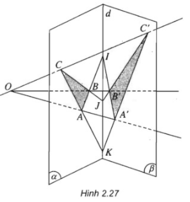
a) I, A’, B’ là ba điểm chung của hai mặt phẳng (OAB) và (β) nên chúng thẳng hàng.
b) I, J, K là ba điểm chung của hai mặt phẳng (ABC) và (A’B’C’) nên chúng thẳng hàng.

a: \(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
\(D\in FS\subset\left(SFE\right)\)
\(B\in SE\subset\left(SFE\right)\)
Do đó: \(BD\subset\left(SFE\right)\)
Ta có: \(O\in BD\subset\left(SEF\right)\)
\(O\in AC\subset\left(ACD\right)\)
Do đó: \(O\in\left(SEF\right)\cap\left(ACD\right)\)
mà \(D\in\left(SEF\right)\cap\left(ACD\right)\)
nên \(\left(SEF\right)\cap\left(ACD\right)=DO\)
b: Xét ΔSDB có
E,F lần lượt là trung điểm của SB,SD
=>EF là đường trung bình của ΔSDB
=>EF//DB
Xét (ABCD) và (AEF) có
BD//EF
\(A\in\left(ABCD\right)\cap\left(AEF\right)\)
Do đó: (ABCD) giao (AEF)=xy, xy đi qua A và xy//BD//EF

.a
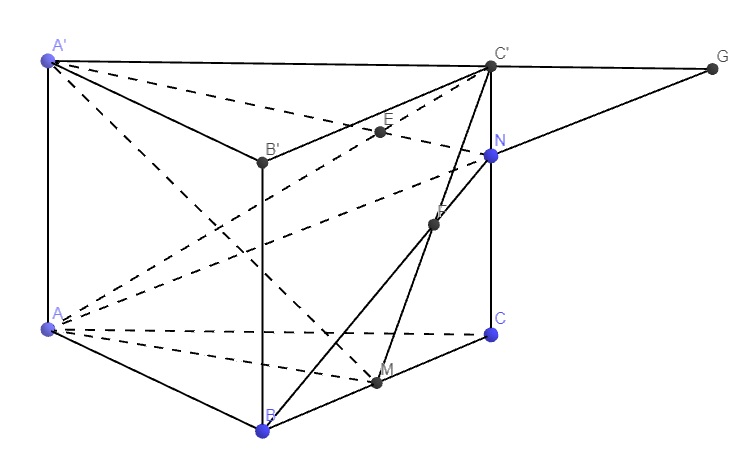
Trong mp (BCC'B') nối MN kéo dài cắt BB' tại D
\(\Rightarrow D\in\left(A'MN\right)\)
Trong mp (ABB'A') nối A'D cắt AB tại I
\(\Rightarrow I=AB\cap\left(A'MN\right)\)
Do CN song song BD, áp dụng Talet:
\(\dfrac{CN}{BD}=\dfrac{CM}{BM}=1\Rightarrow CN=BD\)
\(\Rightarrow\dfrac{BD}{BB'}=\dfrac{CN}{CC'}=\dfrac{2}{3}\)
Do AA' song song BD, áp dụng Talet:
\(\dfrac{IA}{IB}=\dfrac{AA'}{BD}=\dfrac{BB'}{BD}=\dfrac{3}{2}\)
Các câu này quá nhiều đường nét nên mỗi câu 1 hình riêng cho dễ nhìn:
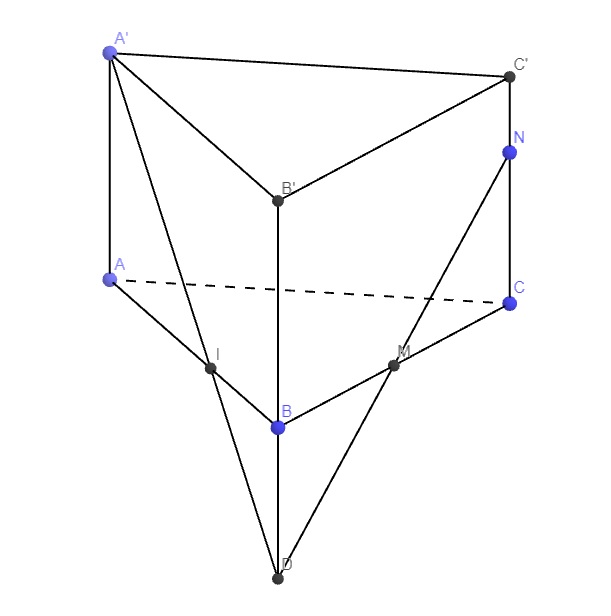
b.
Trong mp (ACC'A'), gọi E là giao điểm A'N và AC'
Trong mp ((BCC'B'), gọi F là giao điểm BN và C'M
\(\Rightarrow EF=\left(AMC'\right)\cap\left(A'NB\right)\)
c.
Trong mp (ACC'A'), kéo dài AN và A'C' cắt nhau tại G
\(\Rightarrow G\in\left(ANB\right)\cap\left(MA'C'\right)\)
\(F=BN\cap C'M\Rightarrow F\in\left(ANB\right)\cap\left(MA'C'\right)\)
\(\Rightarrow FG=\left(ANB\right)\cap\left(MA'C'\right)\)

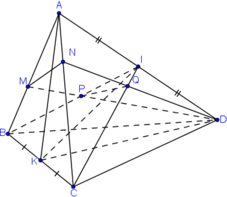
a) Tìm giao tuyến của mp(IBC) và mp(KAD).
Ta có:
K ∈ BC ⇒ K ∈ (IBC) ⇒ K ∈ (IBC) ∩ (KAD)
I ∈ AD ⇒ I ∈ (KAD) ⇒ I ∈ (IBC) ∩ (KAD)
Vậy KI = (IBC) ∩ (KAD)
b) Trong mp(ABD) gọi BI ∩ DM = P
⇒ P ∈ (IBC) ∩ (DMN)
Trong mặt phẳng (ACD) gọi CI ∩ DN = Q
⇒ Q ∈ (IBC) ∩ (DMN)
Vậy (IBC) ∩ (DMN) = PQ.

Ta có:
\(\left. \begin{array}{l}J \in C{\rm{D}}\\C{\rm{D}} \subset \left( {IC{\rm{D}}} \right)\end{array} \right\} \Rightarrow J \in \left( {IC{\rm{D}}} \right)\).
Vậy bốn điểm \(I,J,C,D\) đồng phẳng.
Chọn D.

a) Chứng minh I, K là hai điểm chung của (BIC) và (AKD)
b) Gọi P = CI ∩ DN và Q = BI ∩ DM, chứng minh PQ là giao tuyến cần tìm.
a) \(I\in AD\) nên \(I\in\left(IBC\right)\cap\left(KAD\right)\);
\(K\in BC\) nên \(K\in\left(IBC\right)\cap\left(KAD\right)\).
Vì vậy: \(IK\in\left(IBC\right)\cap\left(KAD\right)\).
b)
Gọi \(P=CI\cap DN\) . Do \(\left\{{}\begin{matrix}P\in CI\\P\in DN\end{matrix}\right.\) nên \(P\in\left(IBC\right)\cap\left(DMN\right)\).
Gọi \(Q=BI\cap MD\). Do \(\left\{{}\begin{matrix}Q\in BI\\Q\in MD\end{matrix}\right.\) nên \(Q\in\left(IBC\right)\cap\left(DMN\right)\).
Vậy PQ là giao tuyến của (IBC) và (DMN).