Hình chữ nhật ABCD có chu vi là 7cm.Đường phân giác góc A cắt DC tại E.Chu vi hình thang ABCE lớn hơn chu vi tam giác ADE là 3cm. Tỉ số giữa chiều rộng và chiều dài của hình chữ nhật ABCD là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 8 2023
Ta có sơ đồ:
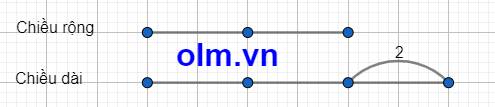
Theo sơ đồ ta có:
Chiều dài của hình chữ nhật là: 2: ( 3 - 2) \(\times\) 3 = 6 (cm)
Chiều rộng của hình chữ nhật là: 6 - 2 = 4 (cm)
Chu vi hình thoi là: 35 \(\times\) 4 = 140 (mm)
140 mm = 14 cm
Chu vi hình chữ nhật là: ( 6 + 4) \(\times\) 2 = 20 (cm)
Tỉ số chu vi hình thoi và hình chữ nhật là: 14: 20 = \(\dfrac{7}{10}\)
Diện tích hình chữ nhật là: 6 \(\times\) 4 = 24 (cm2)
Diện tích hình thoi: thiếu dữ liệu để tính.
23 tháng 8 2021
Bài 2:
a: Xét ΔBAD và ΔBHD có
BA=BH
\(\widehat{ABD}=\widehat{HBD}\)
BD chung
Do đó: ΔBAD=ΔBHD
b: Ta có: ΔBAD=ΔBHD
nên \(\widehat{BAD}=\widehat{BHD}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BHD}=90^0\)
hay DH\(\perp\)BC
NA
7 tháng 11 2021
Nửa chu vi hình chữ nhật là :
28 : 2 = 14 ( cm)
Chiều dài hình chữ nhật là :
(14 + 6) : 2 = 10 ( cm)
Chiều rộng hình chữ nhật là :
10 - 6 = 4 ( cm)
a) Diện tích hình chữ nhật đó là :
10 . 4 = 40 ( cm2 )
( Phần b không có gợi ý nào ạ ?)
Chu vi tam giác ADE là: \(2cm^{2}\)
AE là tia phân giác của góc A=>\(\widehat{DAE}=45^{o}\)\(=>\widehat{DEA}=45^{o}\)
=>\(\Delta ADE\) vuông cân =>AD=AE=2cm(vì AD.AE=4 và AD=AE)
Ta có:
\(S_{ABCE}=\dfrac{(AB+CE).BC}{2}=5\\=>AB+CE=5\\=>AB+AB-2=5\\=>AB=3,5\\=>\dfrac{AD}{AB}=\dfrac{2}{3,5}=\dfrac{4}{7}\)
Vậy tỉ số giữa chiều rộng và chiều dài là \(\dfrac{4}{7}\)