Các bạn chỉ mình, Chỗ phần lời giải chỉ giúp mình tại sao A>0 ạ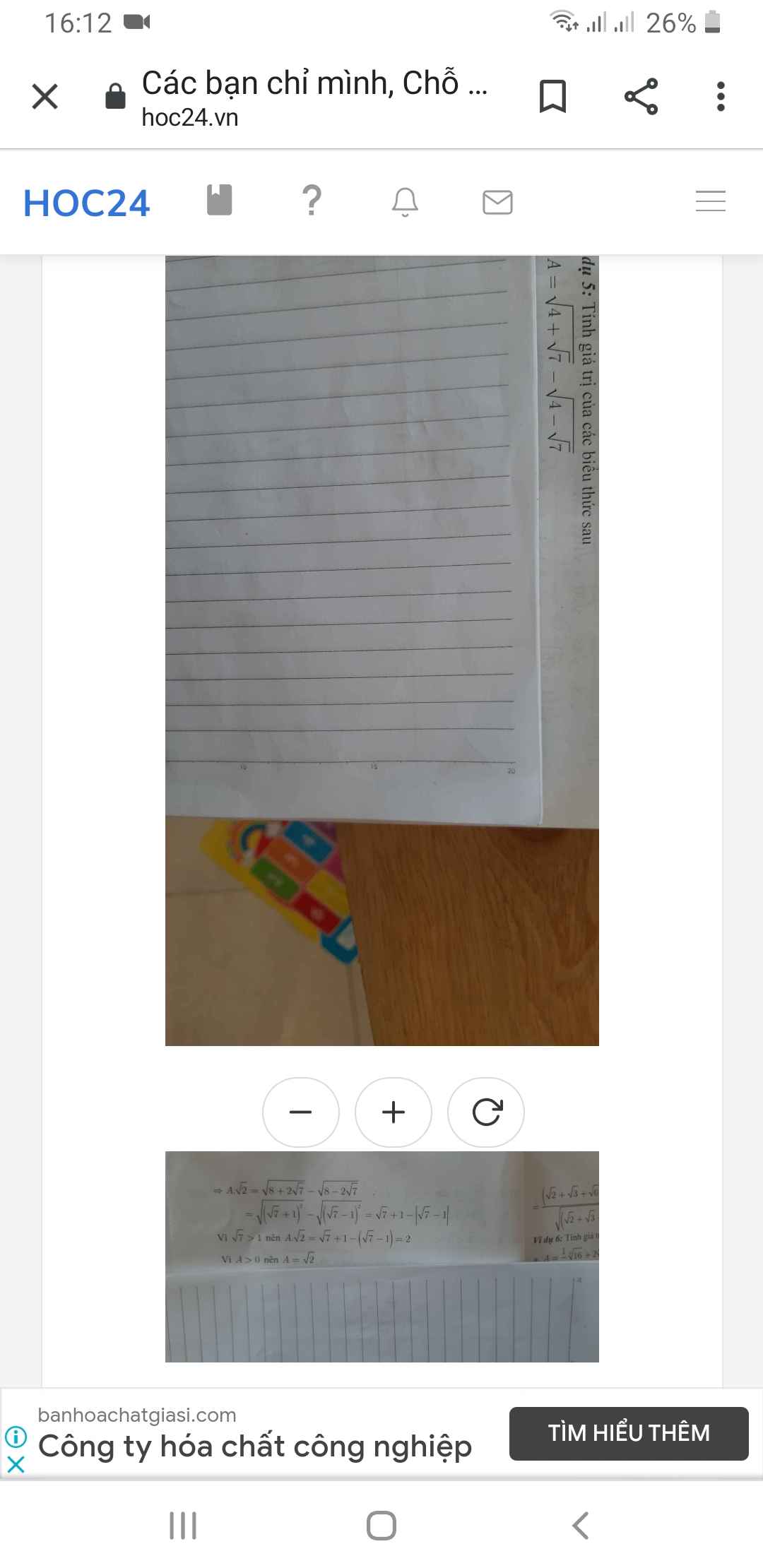
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
C
0
Những câu hỏi liên quan
C
1
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 8 2021
Do \(4+\sqrt{7}>4-\sqrt{7}\)
\(\Rightarrow\sqrt{4+\sqrt{7}}>\sqrt{4-\sqrt{7}}\)
\(\Rightarrow\sqrt{4+\sqrt{7}}-\sqrt{4-\sqrt{7}}>0\)
Hay \(A>0\)
C
2
2 tháng 7 2021
Cacbon không có hóa trị VI, cứ hiểu theo cách này đi nếu em đang học lớp 8 nè!
MN
19 tháng 6 2021
Nôm na như thế này :
Giả sử CT : \(A_xB_y\)
Có khối lượng mol là : M
\(\%A=\dfrac{x\cdot A}{M}\cdot100\%=a\%\)
\(\Rightarrow M=\dfrac{x\cdot A\cdot100\%}{a\%}\left(1\right)\)
\(\%B=\dfrac{B\cdot y}{M}\cdot100\%=b\%\)
\(\Leftrightarrow M=\dfrac{B\cdot y\cdot100\%}{b}\left(2\right)\)
\(\left(1\right),\left(2\right):\)
\(\dfrac{x\cdot A\cdot100\%}{a\%}=\dfrac{y\cdot B\cdot100\%}{b\%}\)
\(\Leftrightarrow\dfrac{x\cdot A}{a}=\dfrac{y\cdot B}{b}\)
\(\Leftrightarrow x\cdot A\cdot b=y\cdot B\cdot a\)
\(\Leftrightarrow\dfrac{x}{y}=\dfrac{B\cdot a}{A\cdot b}=\dfrac{a}{A}:\dfrac{b}{B}\)
Tới đây là hiểu rồi chứ nhỉ !
19 tháng 6 2021
Thanh Lam Là sao bạn chả hiểu gì cả mình đang nói cái CT trên mà bạn đang làm cái gì vậy
AH
Akai Haruma
Giáo viên
15 tháng 5 2021
Lời giải:
$n$ giác có nghĩa là n cạnh. Hình lăng trụ có đáy là đa giác n cạnh. Ở đây, n có hàm ý đại diện cho 1 số như 3 (tam giác), 4 (tứ giác),.....
Bạn vẽ thử 1 hình lăng trụ đứng có n cạnh ra (cho n=3) chả hạn. Khi đó, tương ứng với n cạnh của đáy ta sẽ có n mặt bên. Thêm vào đó có 2 mặt đáy, nên tổng cộng có n+2 mặt.
Công thức ở chỗ khoanh màu cam chỉ là công thức người ta xây dựng nên để áp dụng cho nhanh. Như kiểu công thức diện tích, công thức chu vi thôi.
Trong TH làm bài, bạn chỉ cần vẽ thử 1 lăng trụ đứng (có đáy là tam giác chả hạn) rồi đếm. Đếm TH riêng thì cũng sẽ suy ra TH chung thôi.
25 tháng 6 2021
`a(a+6)+10>0`
`<=>a^2+6a+10>0`
`<=>a^2+6a+9+1>0`
`<=>(a+3)^2+1>0` luôn đúng
TK
20 tháng 7 2021
cái này thì ko nhất thiết phải Cm nha bạn
Câu b kêu tìm x để B ko nhỏ hơn hoặc bằng A
Nghĩa là
\(\dfrac{4}{3-\sqrt{x}}>1\)
\(\Leftrightarrow\dfrac{4}{3-\sqrt{x}}-1>0\)
\(\Leftrightarrow\dfrac{4-\left(3-\sqrt{x}\right)}{3-\sqrt{x}}>0\)
\(\Leftrightarrow\dfrac{\sqrt{x}+1}{3-\sqrt{x}}>0\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\sqrt{x}+1>0\\3-\sqrt{x}>0\end{matrix}\right.\\\left\{{}\begin{matrix}\sqrt{x}+1< 0\left(VL\right)\\3-\sqrt{x}< 0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow3-\sqrt{x}>0\)
\(\Leftrightarrow\sqrt{x}< 3\)
\(\Leftrightarrow x< 9\)
Theo Đk ta có x≥0
Vậy 0≤x<9 thì B ko nhỏ hơn hoặc bằng A
TK
20 tháng 7 2021
\(\sqrt{x}\ge0\Leftrightarrow\sqrt{x}+1\ge1>0\)
Hiển nhiên nhé