Khi đó giá trị của biểu thức
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án B.
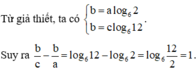
DISCOVERY
Một cách tổng quát chúng ta có các kết quả sau:
1) Cho các số thực dương m, n, p khác 1 và thỏa mãn m.p = n α
Nếu tồn tại các số thực a, b, c thỏa mãn hệ thức ![]()
2) Cho các số thực dương m, n, p khác 1 và thỏa mãn ![]()
Nếu tồn tại các số thực a, b, c thỏa mãn hệ thức ![]()

biến đổi: \(P=1.\left(\dfrac{1}{16x}+\dfrac{1}{4y}+\dfrac{1}{z}\right)=\left(x+y+z\right)\left(\dfrac{1}{16x}+\dfrac{1}{4y}+\dfrac{1}{z}\right)\)
\(P=\left(\dfrac{y}{16x}+\dfrac{x}{4y}\right)+\left(\dfrac{z}{16x}+\dfrac{x}{z}\right)+\left(\dfrac{z}{4y}+\dfrac{y}{z}\right)+\dfrac{21}{16}\)
Áp dụng bất đẳng thức cosi cho từng ngoặc ta được:
\(\dfrac{y}{16x}+\dfrac{x}{4y}\ge2\sqrt{\dfrac{y}{16x}.\dfrac{x}{4y}}=\dfrac{1}{4}\)
hoàn toàn tương tự: \(\dfrac{z}{16x}+\dfrac{x}{z}\ge\dfrac{1}{2}\)
\(\dfrac{z}{4y}+\dfrac{y}{z}\ge1\)
=> P>=49/16
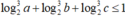 . Khi biểu thức
. Khi biểu thức 



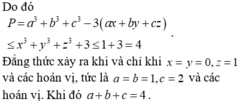


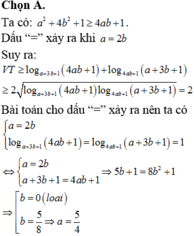


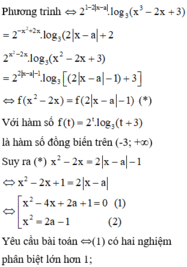
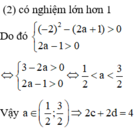
Theo bài ra , ta có :
\(2x^2-2xy+y^2+4x+4=0\)
\(\Rightarrow\left(x^2-2xy+y^2\right)+\left(x^2+4x+4\right)=0\)
\(\Rightarrow\left(x-y\right)^2+\left(x+4\right)^2=0\)
\(\Rightarrow\left\{\begin{matrix}\left(x-y\right)^2=0\\\left(x+4\right)^2=0\end{matrix}\right.\)
\(\Rightarrow\left\{\begin{matrix}x-y=0\\x+4=0\end{matrix}\right.\Rightarrow\left\{\begin{matrix}x=y\\x=-4\end{matrix}\right.\)
\(\Rightarrow x=y=-4\)
Thay x = y = -4 vào A ta được
\(A=x^4+y^4\)
\(\Rightarrow A=\left(-4\right)^4+\left(-4\right)^4=2\times\left(-4\right)^4=512\)
Vậy A = 512
Chúc bạn hok tốt =))
em nhỏ hơn anh một tuổi ák