cho góc xoy trên õ lấy A và trên tia đối oy lấy B để OA = OB. Cm AB // pg của xoy.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
1
Những câu hỏi liên quan
1 tháng 1 2024
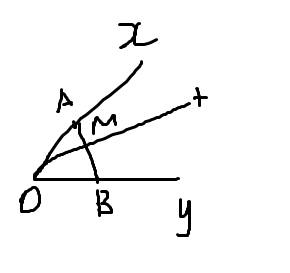
a. OA=OB
⇒ΔOAB cân tại O
mà OM là phân giác góc AOB
nên OM là đường trung tuyến ΔAOB
⇒M là trung điểm AB ⇒MA=MB
b. Xét ΔOAM và ΔOBM, có
OA=OB
OM chung
MA=MB
⇒ΔOAM = ΔOBM
nên OMA=OMB (đpcm)
6 tháng 1 2020
cho tam giác abc có ab = ac tia phân giác góc a cắt bc tại d chứng minh tam giác adb= tam giác adc dh vuông góc với ab dk vuông góc với ac chứng minh dh = dk biết góc bac = 4 nhân với góc abc tính số đo các góc abc
HN
13 tháng 12 2016
Hình bạn tự vẽ nha
Xét \(\Delta AIO\) và \(\Delta BIO\) có:
OI chung
\(\widehat{AOI} = \widehat{BOI}\) (Oz là tia phân giác của \(\widehat{xOy}\) (gt))
OA = OB (gt)
\(\Rightarrow\)\(\Delta AIO = \Delta BIO\) (cgc)
b) Vì \(\Delta AIO = \Delta BIO\) (cmt)
\(\Rightarrow IB=IA\) (2 cạnh tương ứng)
mà OA = OB (gt)
\(\Rightarrow OI\) là đường trung trực của AB
hay \(AB \perp OI\)
Ta có hình vẽ:
A x y O B t
Cho Ot là phân giác của góc xOy
=> góc xOt = góc tOy
Ta có: góc xOy + góc AOB = 1800 (kề bù)
Ta có: góc BAO + góc ABO + góc AOB = 1800 (tổng ba góc của một tam giác)
=> góc xOy = góc BAO + góc ABO
hay góc xOt + góc tOy = góc BAO + góc ABO (1)
Mà góc xOt = góc tOy (cmt) (2)
Ta có: OA = OB => tam giác OAB cân tại O
=> góc BAO = góc ABO (3)
Từ (1),(2),(3) => góc xOt = góc tOy = góc BAO = góc ABO
=> góc BAO = góc xOt
mà hai góc này đang ở vị trí so le trong
=> AB // Ot
-> Ta có: đpcm.