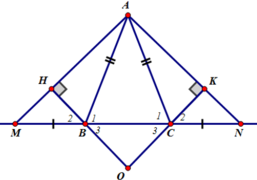
Cho \(\Delta\)ABC cân tại A. Trên tia đối của BC lấy M , trên tia đối của CB lấy N / BM=CN
a, C'm \(\Delta\)ABM=\(\Delta\)ACN
b,Kẻ BC\(\perp\)AM,CK\(\perp\)AN (H\(\in\)AM,K\(\in\)AM ).C'm AH=AC
c, Gọi O là GĐ của HB và KC.C'M \(\Delta\)OBC LÀ \(\Delta\perp\)

 Bn tham khảo nhé!
Bn tham khảo nhé!

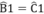
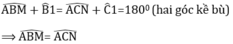
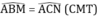
a: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔAHB=ΔAKC
Suy ra: AH=AK
c: Ta có: \(\widehat{OBC}=\widehat{HBM}\)
\(\widehat{OCB}=\widehat{KCN}\)
mà \(\widehat{HBM}=\widehat{KCN}\)
nên \(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O