Cho tam giác Abc cân tại A,các đường phân giác BD của góc B và phân giac CE của góc C(D thuộc AC,E thuộc Ab)
a)chừng minh ED//BC
b)Chừng minh: BEDC là hình thang có đáy nhỏ bằng cạnh bên
viết sơ đồ phân thích tìm lời giải
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : tam giác ABC cân tại A
BD là phân giác của góc ABC
CE là phân giác của góc ACB
=>BD=CE (trong tam giác cân 2 đường phân giác xuất phát từ 2 góc đáy của tam giác bằng nhau . p/s: nếu bạn k bik định lí này bạn có thể chứng minh nhé)
Xét tam giác ABD và tam giác ACE :
BD=CE (cmt)
góc ABD= góc ACE (góc ABC=góc ACB=2 góc ABD= 2 góc ACE)
AB=BC (tam giác ABC cân tại A)
Suy ra: tam giác ABD= tam giác ACE (c-g-c)
=>AD=AE ( 2 cạnh tương ứng)
=>tam giác ADE cân tại A
Mà tam giác ABC cũng cân tại A nên:
góc ABC = góc ACB= góc ADE= goác ADE
Ta lại có: góc ABC và góc AED ở vị trí đồng vị nên:
ED//BC
=>BEDC là hình thang
Mà BD=CE
nên: BEDC là hình thang cân(1)
Ta có: ED//BC => góc DEC = góc ECB
Mà góc ECB= góc DCE ( CE là p/g của góc ACE)
=> góc DEC=góc DCE
=> tam giác DEC cân tại D
=>ED=DC (2)
Từ (1) và (2) suy ra: BEDC là hình thang cân có đáy nhò bằng cạnh bên.
Bài b ko biết hi hi k mình ra
Tiếp câu b .
Có : \(\Delta ABC\) cân tại A
=> \(\widehat{ABC}=\widehat{ACB}\) (1)
Theo tổng 3 góc trong 1 tam giác :
Với \(\Delta ABC\) => \(\widehat{ABC}+\widehat{ACB}+\widehat{A}=180^0\)
=> \(\widehat{ABC}+\widehat{ACB}=130^0\)
Lại có (1)
=> \(\widehat{ABC}=\widehat{ACB}=\frac{130^0}{2}=65^0\)
Vì tứ giác là hình thang cân (chắc cũng biết tứ giác nào nhỉ :v )
=> ED // BC
=> \(\widehat{DEB}+\widehat{EBC}=180^0\)
=> \(\widehat{DEB}=180^0-65^0=115^0\)
Tương tự với góc \(\widehat{EDC}\)

a: Xét ΔABC có
BD là đường phân giác
nên \(\dfrac{AD}{DC}=\dfrac{AB}{BC}=\dfrac{AC}{BC}\left(1\right)\)
Xét ΔACB có
CE là đường phân giác
nên \(\dfrac{AE}{EB}=\dfrac{AC}{BC}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{AE}{EB}=\dfrac{AD}{DC}\)
hay ED//BC
Xét tứ giác BEDC có ED//BC
nên BEDC là hình thang
mà \(\widehat{EBC}=\widehat{DCB}\)
nên BEDC là hình thang cân

Ta có : tam giác ABC cân tại A
BD là phân giác của góc ABC
CE là phân giác của góc ACB
=>BD=CE (trong tam giác cân 2 đường phân giác xuất phát từ 2 góc đáy của tam giác bằng nhau . p/s: nếu bạn k bik định lí này bạn có thể chứng minh nhé)
Xét tam giác ABD và tam giác ACE :
BD=CE (cmt)
góc ABD= góc ACE (góc ABC=góc ACB=2 góc ABD= 2 góc ACE)
AB=BC (tam giác ABC cân tại A)
Suy ra: tam giác ABD= tam giác ACE (c-g-c)
=>AD=AE ( 2 cạnh tương ứng)
=>tam giác ADE cân tại A
Mà tam giác ABC cũng cân tại A nên:
góc ABC = góc ACB= góc ADE= goác ADE
Ta lại có: góc ABC và góc AED ở vị trí đồng vị nên:
ED//BC
=>BEDC là hình thang
Mà BD=CE
nên: BEDC là hình thang cân(1)
Ta có: ED//BC => góc DEC = góc ECB
Mà góc ECB= góc DCE ( CE là p/g của góc ACE)
=> góc DEC=góc DCE
=> tam giác DEC cân tại D
=>ED=DC (2)
Từ (1) và (2) suy ra: BEDC là hình thang cân có đáy nhò bằng cạnh bên.
Ta có : tam giác ABC cân tại A
BD là phân giác của góc ABC
CE là phân giác của góc ACB
=>BD=CE (trong tam giác cân 2 đường phân giác xuất phát từ 2 góc đáy của tam giác bằng nhau . p/s: nếu bạn k bik định lí này bạn có thể chứng minh nhé)
Xét tam giác ABD và tam giác ACE :
BD=CE (cmt)
góc ABD= góc ACE (góc ABC=góc ACB=2 góc ABD= 2 góc ACE)
AB=BC (tam giác ABC cân tại A)
Suy ra: tam giác ABD= tam giác ACE (c-g-c)
=>AD=AE ( 2 cạnh tương ứng)
=>tam giác ADE cân tại A
Mà tam giác ABC cũng cân tại A nên:
góc ABC = góc ACB= góc ADE= goác ADE
Ta lại có: góc ABC và góc AED ở vị trí đồng vị nên:
ED//BC
=>BEDC là hình thang
Mà BD=CE
nên: BEDC là hình thang cân(1)
Ta có: ED//BC => góc DEC = góc ECB
Mà góc ECB= góc DCE ( CE là p/g của góc ACE)
=> góc DEC=góc DCE
=> tam giác DEC cân tại D
=>ED=DC (2)
Từ (1) và (2) suy ra: BEDC là hình thang cân có đáy nhò bằng cạnh bên.

Ta có : tam giác ABC cân tại A
BD là phân giác của góc ABC
CE là phân giác của góc ACB
=>BD=CE (trong tam giác cân 2 đường phân giác xuất phát từ 2 góc đáy của tam giác bằng nhau . p/s: nếu bạn k bik định lí này bạn có thể chứng minh nhé)
Xét tam giác ABD và tam giác ACE :
BD=CE (cmt)
góc ABD= góc ACE (góc ABC=góc ACB=2 góc ABD= 2 góc ACE)
AB=BC (tam giác ABC cân tại A)
Suy ra: tam giác ABD= tam giác ACE (c-g-c)
=>AD=AE ( 2 cạnh tương ứng)
=>tam giác ADE cân tại A
Mà tam giác ABC cũng cân tại A nên:
góc ABC = góc ACB= góc ADE= goác ADE
Ta lại có: góc ABC và góc AED ở vị trí đồng vị nên:
ED//BC
=>BEDC là hình thang
Mà BD=CE
nên: BEDC là hình thang cân(1)
Ta có: ED//BC => góc DEC = góc ECB
Mà góc ECB= góc DCE ( CE là p/g của góc ACE)
=> góc DEC=góc DCE
=> tam giác DEC cân tại D
=>ED=DC (2)
Từ (1) và (2) suy ra: BEDC là hình thang cân có đáy nhò bằng cạnh bên.
Bạn tự vẽ hình nha ==''
ABD = DBC = ABC/2 (BD là tia phân giác của ABC)
ACE = ECB = ACB/2 (CE là tia phân giác của ACB)
mà ABC = ACB (tam giác ABC cân tại A)
=> ABD = ACE
Xét tam giác ABD và tam giác ACE có:
BAC là góc chung
AB = AC
ABD = ACE (chứng minh trên)
=> Tam giác ABD = Tam giác ACE (g.c.g)
=> AD = AE (2 cạnh tương ứng)
=> Tam giác ADE cân tại A
=> AED = 900 - EAD/2
mà ABC = 900 - BAC/2 (tam giác ABC cân tại A)
=> AED = ABC
mà 2 góc này ở vị trí đồng vị
=> ED // BC
=> BEDC là hình thang
mà ABC = ACB (tam giác ABC cân tại A)
=> BEDC là hình thang cân
ED // BC
=> EDB = DBC (2 góc so le trong)
mà DBC = ABD (BD là tia phân giác của ABC)
=> EDB = ABD
=> Tam giác EBD cân tại E
=> EB = ED
=> BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.

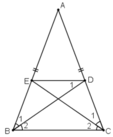
- Chứng minh tứ giác BCDE là hình thang cân:
+ ΔABC cân tại A 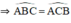
BD là phân giác của 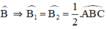
CE là phân giác của 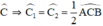
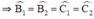
+ Xét ΔAEC và ΔADB có:
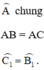
⇒ ΔAEC = ΔADB
⇒ AE = AD
Vậy tam giác ABC cân tại A có AE = AD
Theo kết quả bài 15a) suy ra BCDE là hình thang cân.
- Chứng minh ED = EB.
ED // BC ⇒ 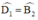 (Hai góc so le trong)
(Hai góc so le trong)
Mà 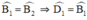 ⇒ ΔEDB cân tại E ⇒ ED = EB.
⇒ ΔEDB cân tại E ⇒ ED = EB.
Vậy ta có EBCD là hình thang cân có đáy nhỏ bằng cạnh bên.

a
Từ giả thiết có: ΔABC cân tại A, BD và CE là phân giác.
=> BD và CE là 2 đường trung tuyến hay ED là đường trung bình của ΔABC.
=> BD//CE (1)
Xét ΔBDA và ΔCEA có:
\(\widehat{A}\) chung
AE = AD (gt)
AB = AC (gt)
=> ΔBDA = ΔCEA (c.g.c)
=> `EC=DB` (2)
Từ (1), (2) => BEDC là hình thang cân.
b
ΔABC cân => \(\widehat{B}=\widehat{C}=50^o\)
Tổng 4 góc của tứ giác là `360^o` mà `BEDC` là hình thang cân.
=> \(\widehat{E}=\widehat{D}=\dfrac{360^o-100^o}{2}=130^o\)
a) Xét ΔABC có
BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AD}{DC}=\dfrac{AB}{BC}\)(1)
Xét ΔABC có
CE là đường phân giác ứng với cạnh AB(gt
nên \(\dfrac{AE}{EB}=\dfrac{AC}{BC}\left(2\right)\)
Ta có: ΔABC cân tại A
nên \(AB=AC\left(3\right)\)
Từ (1), (2) và (3) suy ra \(\dfrac{AE}{EB}=\dfrac{AD}{DC}\)
hay ED//BC
b: Xét tứ giác EDCB có ED//BC
nên EDCB là hình thang
mà \(\widehat{EBC}=\widehat{DCB}\)
nên EDCB là hình thang cân
Xét ΔDEC có \(\widehat{DEC}=\widehat{DCE}\left(=\widehat{ECB}\right)\)
nên ΔDEC cân tại D
Suy ra: DE=DC
mà DC=EB
nên DE=DC=EB