Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
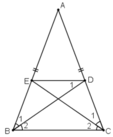
Ta có : tam giác ABC cân tại A
BD là phân giác của góc ABC
CE là phân giác của góc ACB
=>BD=CE (trong tam giác cân 2 đường phân giác xuất phát từ 2 góc đáy của tam giác bằng nhau . p/s: nếu bạn k bik định lí này bạn có thể chứng minh nhé)
Xét tam giác ABD và tam giác ACE :
BD=CE (cmt)
góc ABD= góc ACE (góc ABC=góc ACB=2 góc ABD= 2 góc ACE)
AB=BC (tam giác ABC cân tại A)
Suy ra: tam giác ABD= tam giác ACE (c-g-c)
=>AD=AE ( 2 cạnh tương ứng)
=>tam giác ADE cân tại A
Mà tam giác ABC cũng cân tại A nên:
góc ABC = góc ACB= góc ADE= goác ADE
Ta lại có: góc ABC và góc AED ở vị trí đồng vị nên:
ED//BC
=>BEDC là hình thang
Mà BD=CE
nên: BEDC là hình thang cân(1)
Ta có: ED//BC => góc DEC = góc ECB
Mà góc ECB= góc DCE ( CE là p/g của góc ACE)
=> góc DEC=góc DCE
=> tam giác DEC cân tại D
=>ED=DC (2)
Từ (1) và (2) suy ra: BEDC là hình thang cân có đáy nhò bằng cạnh bên.
Bài b ko biết hi hi k mình ra
Tiếp câu b .
Có : \(\Delta ABC\) cân tại A
=> \(\widehat{ABC}=\widehat{ACB}\) (1)
Theo tổng 3 góc trong 1 tam giác :
Với \(\Delta ABC\) => \(\widehat{ABC}+\widehat{ACB}+\widehat{A}=180^0\)
=> \(\widehat{ABC}+\widehat{ACB}=130^0\)
Lại có (1)
=> \(\widehat{ABC}=\widehat{ACB}=\frac{130^0}{2}=65^0\)
Vì tứ giác là hình thang cân (chắc cũng biết tứ giác nào nhỉ :v )
=> ED // BC
=> \(\widehat{DEB}+\widehat{EBC}=180^0\)
=> \(\widehat{DEB}=180^0-65^0=115^0\)
Tương tự với góc \(\widehat{EDC}\)
a: Xét ΔABC có
BD là đường phân giác
nên \(\dfrac{AD}{DC}=\dfrac{AB}{BC}=\dfrac{AC}{BC}\left(1\right)\)
Xét ΔACB có
CE là đường phân giác
nên \(\dfrac{AE}{EB}=\dfrac{AC}{BC}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{AE}{EB}=\dfrac{AD}{DC}\)
hay ED//BC
Xét tứ giác BEDC có ED//BC
nên BEDC là hình thang
mà \(\widehat{EBC}=\widehat{DCB}\)
nên BEDC là hình thang cân
Ta có : tam giác ABC cân tại A
BD là phân giác của góc ABC
CE là phân giác của góc ACB
=>BD=CE (trong tam giác cân 2 đường phân giác xuất phát từ 2 góc đáy của tam giác bằng nhau . p/s: nếu bạn k bik định lí này bạn có thể chứng minh nhé)
Xét tam giác ABD và tam giác ACE :
BD=CE (cmt)
góc ABD= góc ACE (góc ABC=góc ACB=2 góc ABD= 2 góc ACE)
AB=BC (tam giác ABC cân tại A)
Suy ra: tam giác ABD= tam giác ACE (c-g-c)
=>AD=AE ( 2 cạnh tương ứng)
=>tam giác ADE cân tại A
Mà tam giác ABC cũng cân tại A nên:
góc ABC = góc ACB= góc ADE= goác ADE
Ta lại có: góc ABC và góc AED ở vị trí đồng vị nên:
ED//BC
=>BEDC là hình thang
Mà BD=CE
nên: BEDC là hình thang cân(1)
Ta có: ED//BC => góc DEC = góc ECB
Mà góc ECB= góc DCE ( CE là p/g của góc ACE)
=> góc DEC=góc DCE
=> tam giác DEC cân tại D
=>ED=DC (2)
Từ (1) và (2) suy ra: BEDC là hình thang cân có đáy nhò bằng cạnh bên.
Ta có : tam giác ABC cân tại A
BD là phân giác của góc ABC
CE là phân giác của góc ACB
=>BD=CE (trong tam giác cân 2 đường phân giác xuất phát từ 2 góc đáy của tam giác bằng nhau . p/s: nếu bạn k bik định lí này bạn có thể chứng minh nhé)
Xét tam giác ABD và tam giác ACE :
BD=CE (cmt)
góc ABD= góc ACE (góc ABC=góc ACB=2 góc ABD= 2 góc ACE)
AB=BC (tam giác ABC cân tại A)
Suy ra: tam giác ABD= tam giác ACE (c-g-c)
=>AD=AE ( 2 cạnh tương ứng)
=>tam giác ADE cân tại A
Mà tam giác ABC cũng cân tại A nên:
góc ABC = góc ACB= góc ADE= goác ADE
Ta lại có: góc ABC và góc AED ở vị trí đồng vị nên:
ED//BC
=>BEDC là hình thang
Mà BD=CE
nên: BEDC là hình thang cân(1)
Ta có: ED//BC => góc DEC = góc ECB
Mà góc ECB= góc DCE ( CE là p/g của góc ACE)
=> góc DEC=góc DCE
=> tam giác DEC cân tại D
=>ED=DC (2)
Từ (1) và (2) suy ra: BEDC là hình thang cân có đáy nhò bằng cạnh bên.
Ta có : tam giác ABC cân tại A
BD là phân giác của góc ABC
CE là phân giác của góc ACB
=>BD=CE (trong tam giác cân 2 đường phân giác xuất phát từ 2 góc đáy của tam giác bằng nhau . p/s: nếu bạn k bik định lí này bạn có thể chứng minh nhé)
Xét tam giác ABD và tam giác ACE :
BD=CE (cmt)
góc ABD= góc ACE (góc ABC=góc ACB=2 góc ABD= 2 góc ACE)
AB=BC (tam giác ABC cân tại A)
Suy ra: tam giác ABD= tam giác ACE (c-g-c)
=>AD=AE ( 2 cạnh tương ứng)
=>tam giác ADE cân tại A
Mà tam giác ABC cũng cân tại A nên:
góc ABC = góc ACB= góc ADE= goác ADE
Ta lại có: góc ABC và góc AED ở vị trí đồng vị nên:
ED//BC
=>BEDC là hình thang
Mà BD=CE
nên: BEDC là hình thang cân(1)
Ta có: ED//BC => góc DEC = góc ECB
Mà góc ECB= góc DCE ( CE là p/g của góc ACE)
=> góc DEC=góc DCE
=> tam giác DEC cân tại D
=>ED=DC (2)
Từ (1) và (2) suy ra: BEDC là hình thang cân có đáy nhò bằng cạnh bên.
Bạn tự vẽ hình nha ==''
ABD = DBC = ABC/2 (BD là tia phân giác của ABC)
ACE = ECB = ACB/2 (CE là tia phân giác của ACB)
mà ABC = ACB (tam giác ABC cân tại A)
=> ABD = ACE
Xét tam giác ABD và tam giác ACE có:
BAC là góc chung
AB = AC
ABD = ACE (chứng minh trên)
=> Tam giác ABD = Tam giác ACE (g.c.g)
=> AD = AE (2 cạnh tương ứng)
=> Tam giác ADE cân tại A
=> AED = 900 - EAD/2
mà ABC = 900 - BAC/2 (tam giác ABC cân tại A)
=> AED = ABC
mà 2 góc này ở vị trí đồng vị
=> ED // BC
=> BEDC là hình thang
mà ABC = ACB (tam giác ABC cân tại A)
=> BEDC là hình thang cân
ED // BC
=> EDB = DBC (2 góc so le trong)
mà DBC = ABD (BD là tia phân giác của ABC)
=> EDB = ABD
=> Tam giác EBD cân tại E
=> EB = ED
=> BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.
- Chứng minh tứ giác BCDE là hình thang cân:
+ ΔABC cân tại A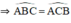 
BD là phân giác của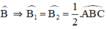 
CE là phân giác của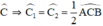 
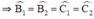
+ Xét ΔAEC và ΔADB có:
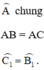
⇒ ΔAEC = ΔADB
⇒ AE = AD
Vậy tam giác ABC cân tại A có AE = AD
Theo kết quả bài 15a) suy ra BCDE là hình thang cân.
- Chứng minh ED = EB.
ED // BC ⇒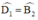 
(Hai góc so le trong)
Mà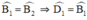 
⇒ ΔEDB cân tại E ⇒ ED = EB.
Vậy ta có EBCD là hình thang cân có đáy nhỏ bằng cạnh bên.
a
Từ giả thiết có: ΔABC cân tại A, BD và CE là phân giác.
=> BD và CE là 2 đường trung tuyến hay ED là đường trung bình của ΔABC.
=> BD//CE (1)
Xét ΔBDA và ΔCEA có:
\(\widehat{A}\) chung
AE = AD (gt)
AB = AC (gt)
=> ΔBDA = ΔCEA (c.g.c)
=> `EC=DB` (2)
Từ (1), (2) => BEDC là hình thang cân.
b
ΔABC cân => \(\widehat{B}=\widehat{C}=50^o\)
Tổng 4 góc của tứ giác là `360^o` mà `BEDC` là hình thang cân.
=> \(\widehat{E}=\widehat{D}=\dfrac{360^o-100^o}{2}=130^o\)
a) Xét ΔABC có
BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AD}{DC}=\dfrac{AB}{BC}\)(1)
Xét ΔABC có
CE là đường phân giác ứng với cạnh AB(gt
nên \(\dfrac{AE}{EB}=\dfrac{AC}{BC}\left(2\right)\)
Ta có: ΔABC cân tại A
nên \(AB=AC\left(3\right)\)
Từ (1), (2) và (3) suy ra \(\dfrac{AE}{EB}=\dfrac{AD}{DC}\)
hay ED//BC
b: Xét tứ giác EDCB có ED//BC
nên EDCB là hình thang
mà \(\widehat{EBC}=\widehat{DCB}\)
nên EDCB là hình thang cân
Xét ΔDEC có \(\widehat{DEC}=\widehat{DCE}\left(=\widehat{ECB}\right)\)
nên ΔDEC cân tại D
Suy ra: DE=DC
mà DC=EB
nên DE=DC=EB