:Cho hình chữ nhật ABCD , AB = 3a , AD = a .Tính |vectoAD + 2vectoBC|
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\left|\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AC}\right|=2\cdot AC=2\cdot5=10\)
b: \(\left|\overrightarrow{AM}+\overrightarrow{AN}\right|=\left|\dfrac{\overrightarrow{AB}+\overrightarrow{AC}}{2}+\dfrac{\overrightarrow{AD}+\overrightarrow{AC}}{2}\right|\)
\(=\left|\dfrac{3\cdot\overrightarrow{AC}}{2}\right|=\dfrac{3}{2}AC=\dfrac{3}{2}\cdot5=\dfrac{15}{2}=7.5\)

(SD;(ABCD))=(DS;DA)=góc SDA
tan SDA=SA/AD=3/2
=>góc SDA=56 độ

** M là trung điểm của AB đúng không bạn?
a.
\(|\overrightarrow{AM}+\overrightarrow{AB}|=|\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AB}|=\frac{3}{2}|\overrightarrow{AB}|=\frac{3}{2}.3a=\frac{9a}{2}\)
b.
\(|\overrightarrow{AB}+\overrightarrow{CD}|=|\overrightarrow{AB}+\overrightarrow{BA}|=|\overrightarrow{0}|=0\)
c.Trên $CD$ lấy $K$ sao cho $CK=a$. Khi đó:
\(|\overrightarrow{DN}+\overrightarrow{BN}|=|\overrightarrow{DN}+\overrightarrow{KD}|=|\overrightarrow{KN}|=KN=\sqrt{a^2+a^2}=\sqrt{2}a\)

Chọn A.
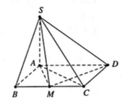
Gắn tọa độ Oxyz, với A(0;0;0), B(1;0;0), D(0;3;0), S(0;0;1)
Khi đó C ( 1 ; 3 ; 0 ) ⇒ Trung điểm M của BC là M ( 1 ; 3 2 ; 0 ) .
Ta có
SM → = ( 1 ; 3 2 ; - 1 ) , SD → = ( 0 ; 3 ; - 1 ) ⇒ [ SM → ; SD → ] = ( 3 2 ; 1 ; 3 ) .
Suy ra n ⃗ ( SDM ) = ( 3 2 ; 1 ; 3 ) mà n ⃗ ( ABCD ) = n ⃗ ( Oxy ) = ( 0 ; 0 ; 1 ) ,
ta được
cos ( SDM ^ ) ; ( ABCD ) = n → ( SDM ) . n → ( ABCD ) n → ( SDM ) . n → ( ABCD ) = 6 7 .

Đáp án D
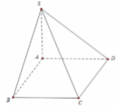
Ta có S A = S B 2 − A B 2 = 4 a
Khi đó:
V S . A B C D = 1 3 S A . S A B C D = 1 3 .4 a .6 a 2 = 8 a 3

Đáp án B
Ta có S A B C D = 2 a 2 ⇒ S A = 3 V S A B C D = a
Lại có S B ; A B C D ^ = S B A ^ , mặt khác tan S B A ^ = 1 ⇒ S B A ^ = 45 °
ta có
\(M=\left|\overrightarrow{AD}+2\overrightarrow{BC}\right|=\left|\overrightarrow{AD}+2\overrightarrow{AD}\right|=3\left|\overrightarrow{AD}\right|=3AD=3a\)
Vậy độ dài của \(\left|\overrightarrow{AD}+2\overrightarrow{BC}\right|=3a\)