Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
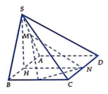
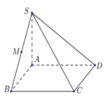
Gọi H là trung điểm của cạnh AB. Khi đó S H ⊥ ( A B C D )
Ta có S H ⊥ A B ; A B ⊥ H N ; H N ⊥ S H và S H = 3
Chọn hệ trục tọa độ Oxyz sao cho H trùng với O, B thuộc tia Ox, N thuộc tia Oy và S thuộc tia Oz. Khi đó:
B ( 1 ; 0 ; 0 ) ; A ( - 1 ; 0 ; 0 ) ; N ( 0 ; 2 3 ; 0 ) ; C ( 1 ; 2 3 ; 0 ) ; D ( - 1 ; 2 3 ; 0 ) ; S ( 0 ; 0 ; 3 ) ; M ( - 1 2 ; 0 ; 3 2 ) ; P ( 1 ; 3 ; 0 )
Mặt phẳng (SCD) nhận n 1 → = - 3 6 C D → , S C → = 0 ; 1 ; 2 làm một vectơ pháp tuyến; mặt phẳng (MNP) nhận n 2 → = - 2 3 3 M N → , M P → = 3 ; 1 ; 5 làm một vectơ pháp tuyến.
Gọi ∅ là góc tạo bởi hai mặt phẳng (MNP) và (SCD) thì
cos ∅ = n 1 → . n 2 → n 1 → . n 2 → = 11 145 145

Chọn đáp án B.
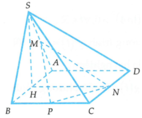

Chọn hệ trục tọa độ Oxyz sao cho H trùng với O, B thuộc tia Ox, N thuộc tia Oy và S thuộc tia Oz. Khi đó:


Đáp án C
Gọi O là trung điểm của SD. Ta có: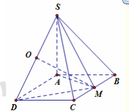
A D = D M = a 2 và A D = 2 a ⇒ A M ⊥ D M
Lại có D M ⊥ S A ⇒ D M ⊥ S A M ⇒ D M ⊥ S M
Vì tam giác SAD vuông tại A nên OS = OD = OA. Tương tự với tam giác SMD nên OS = OD = OM.
Vậy O là tâm mặt cầu ngoại tiếp hình chóp S.ADM. Khi đó R = S D 2 = S A 2 + D A 2 2 = a 6 2 .

Đáp án A.
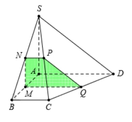
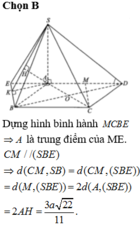
Gọi N, Q lần lượt là trung điểm của AB, CD ⇒ M N ⊥ A B M Q ⊥ A B .
Qua N kẻ đường thẳng song song với BC, cắt SC tại P.
Suy ra thiết diện của mặt phẳng α và hình chóp là MNPQ.
Vì MQ là đường trung bình của hình tháng ABCD ⇒ M Q = 3 a 2 .
MN là đường trung bình của tam giác SAB ⇒ M N = S A 2 = a .
NP là đường trung bình của tam giác SBC ⇒ N P = B C 2 = a 2 .
Vậy diện tích hình thang MNPQ là S M N P Q = M N . N P + M Q 2 = a 2 a 2 + 3 a 2 = a 2 .

Đáp án A
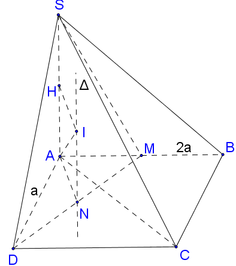
Gọi N là trung điểm của MD, khi đó N là tâm đường tròn ngoại tiếp tam giác vuông ADM.
Dựng đường thẳng Δ đi qua N và song song với SA⇒Δ là trục đường tròn ngoại tiếp tam giác ADM.
Dựng mặt phẳng trung trực (P) của SA, P ∩ Δ = I , khi đó I là tâm của mặt cầu ngoại tiếp hình chóp SADM, bán kính R = IA .
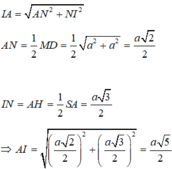
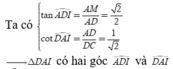
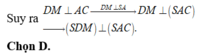
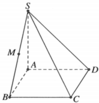
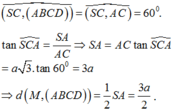
Chọn A.
Gắn tọa độ Oxyz, với A(0;0;0), B(1;0;0), D(0;3;0), S(0;0;1)
Khi đó C ( 1 ; 3 ; 0 ) ⇒ Trung điểm M của BC là M ( 1 ; 3 2 ; 0 ) .
Ta có
SM → = ( 1 ; 3 2 ; - 1 ) , SD → = ( 0 ; 3 ; - 1 ) ⇒ [ SM → ; SD → ] = ( 3 2 ; 1 ; 3 ) .
Suy ra n ⃗ ( SDM ) = ( 3 2 ; 1 ; 3 ) mà n ⃗ ( ABCD ) = n ⃗ ( Oxy ) = ( 0 ; 0 ; 1 ) ,
ta được
cos ( SDM ^ ) ; ( ABCD ) = n → ( SDM ) . n → ( ABCD ) n → ( SDM ) . n → ( ABCD ) = 6 7 .