Cho và
. Giá trị của
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 3 2017
Chọn A.
Giả sử các giá trị của mẫu số liệu là a; b; c; d với 0 < a < b < c < d và a; b; c;d là số tự nhiên.
+ Ta có 
Mà số trung bình là 6 nên a + b + c + d = 24
Suy ra a + d = 14
+ Ta có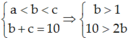 
hay 1 < b < 5 mà b là số tự nhiên nên b = 2; 3; 4
+ Nếu b = 2 thì c = 8, mà 0 < a < b; a là số tự nhiên nên a = 1 và d = 13
Khi đó các giá trị của mẫu số liệu là 1; 2; 8; 13
+ Nếu b = 3 thì c = 7, mà 0 < a < b; a số tự nhiên nên có 2 khả năng xảy ra: a = 1 ; d = 13 hoặc a = 2 ; d = 12
Khi đó có hai mẫu số liệu thỏa đề bài có giá trị là 1;3;7;13 và 2;3;7;12
+ Nếu b = 4 thì c = 6, mà 0 < a < b; a là số tự nhiên nên có 3 khả năng xảy ra:
a = 1; d = 13 hoặc a = 2 ; d = 12 hoặc a = 3 ; d = 11
Khi đó có ba mẫu số liệu thỏa đề bài có giá trị là 1;4;6;13 hoặc 2;4;6;12 hoặc 3;4;6;11
Suy ra với mẫu số liệu có các giá trị là 3;4;6;11 thì hiệu của giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đạt giá trị nhỏ nhất.
CM
25 tháng 2 2017
Đáp án A
Đặt t = log 1 3 a với a ∈ 1 9 ; 3 ⇒ t ∈ - 1 ; 2 .
Khi đó P = 9 log 1 3 3 a 3 - log 1 3 a 3 + 1 = 1 3 log 1 3 a 3 - 3 log 1 3 a + 1 ⇒ P = f ( t ) = t 3 3 - 3 t + 1
Xét hàm số f t = t 3 3 - 3 t + 1 trên đoạn [-1;2] ta có:
f ' t = t 2 - 3 ; f ' t = 0 ⇔ t 2 = 3 - 1 ≤ t ≤ 2 ⇔ t = 3
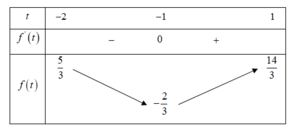
Tính các giá trị f - 1 = 11 3 ; f 2 = - 7 3 ; f 3 = 1 - 2 3
Vậy giá trị lớn nhất của f(t) là f - 1 = 11 3 và giá trị nhỏ nhất của f(t) là f 3 = 1 - 2 3
Do đó 3 M + 5 m = 3 . 11 3 + 5 1 - 2 3 = 16 - 10 3 = - 1 , 32
13 tháng 11 2021
Cho biểu thức P = x(x – y) + y(x + y) – y 2 . Khẳng định nào sau đây là đúng?
A. Giá trị biểu thức P không phụ thuộc vào giá trị của x và y.
B. Giá trị biểu thức P phụ thuộc vào giá trị của x và y
C. Giá trị biểu thức P chỉ phụ thuộc vào giá trị của x.
D. Giá trị biểu thức P chỉ phụ thuộc vào giá trị của y.
Bài làm:
\(P=x\left(x-y\right)+y\left(x+y\right)-y^2\)
\(=x^2-xy+xy+y^2-y^2\)
\(=x^2\)
Vậy biểu thức P chỉ phụ thuộc vào giá trị x.
Chọn C.
1 tháng 12 2021
Ta có \(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{x_1+x_1}{y_1+y_2}=\dfrac{15}{20}=\dfrac{3}{4}\)
\(\Rightarrow\left\{{}\begin{matrix}y_1=\dfrac{4}{3}x_1\\y_2=\dfrac{4}{3}x_2\end{matrix}\right.\Rightarrow y=\dfrac{4}{3}x\)
Với \(x=1,5=\dfrac{3}{2}\Rightarrow y=\dfrac{4}{3}\cdot\dfrac{3}{2}=2\)
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
Thay giá trị \(x = - 1\) và \(y = - 2\) vào các biểu thức đã cho, ta có:
\(A = - ( - 4x + 3y) = - ( - 4. - 1 + 3. - 2) = - (4 + - 6) = - ( - 2) = 2\).
\(B = 4x + 3y = 4. - 1 + 3. - 2 = - 4 + - 6 = - 10\).
\(C = 4x - 3y = 4.( - 1) - 3.( - 2) = - 4 - - 6 = - 4 + 6 = 2\).
Ta thấy 2 ≠ -2 = 2. Do vậy, khi thay giá trị \(x = - 1\) và \(y = - 2\) vào các biểu thức đã cho ta thấy giá trị của các biểu thức A và C bằng nhau.
Vậy bạn Bình nói đúng.
và 
. Tính giá trị của biểu thức 
. B. 
. C. 
. D. 
.
.
đạt giá trị nhỏ nhất là 
. B. 
. D. 
.
.
. B. 
. D. 
/
thỏa mãn 
B. 
C. 
D. 
?
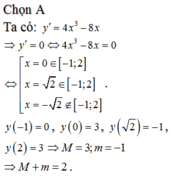
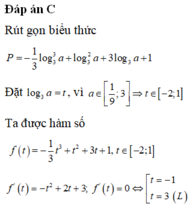
Ta có:\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\) và a+2b+3c=44,2
\(\Rightarrow\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+2b+3c}{3+4\cdot2+5\cdot3}=\frac{44,2}{26}=\frac{17}{10}=1,7\)(T/C...)
\(\Rightarrow a=1,7\cdot3=5,1;b=4\cdot1,7=6,8;c=5\cdot1,7=8,5\)
\(\Rightarrow a+b-c=5,1+6,8-8,5=3,4\)