tìm tỉ số lượng giác của góc a , biết
a/ cos a = 0,8 b/ tga = \(\dfrac{1}{3}\)
( cô mình không cho hình sẵn )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
1
10 tháng 9 2019
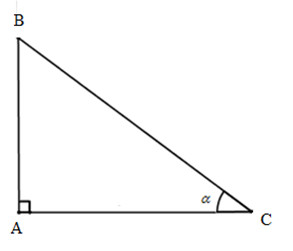
Vì tam giác ABC vuông tại A nên góc C nhọn. Vì thế:
sinC>0;cosC>0;tanC>0;cotC>0sinC>0;cosC>0;tanC>0;cotC>0
Vì hai góc B và C phụ nhau nên sinC = cosB = 0,8.
Ta có:
Sin2C+cos2C=1Sin2C+cos2C=1
⇒cos2C=1−sin2C=1−(0,8)2=0,36⇒cos2C=1−sin2C=1−(0,8)2=0,36
⇒cosC=0,6;⇒cosC=0,6;
tgC=sinCcosC=0,80,6=43;tgC=sinCcosC=0,80,6=43;
cotgC=cosCsinC=0,60,8=34
21 tháng 8 2017
Làm tiêu biểu 1 bài thôi nhé. Các bài còn lại tương tự
a/ sin a = 0,8
Ta có: sin2 a + cos2 a = 1
=> cos2 a = 1 - sin2 a = 1 - 0,82 = 0,36
\(\Rightarrow\orbr{\begin{cases}cos\:a=0,6\\cos\:a=-0,6\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}tan\:a=\frac{4}{3}\\tan\:a=-\frac{4}{3}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}cot\:a=\frac{3}{4}\\cot\:a=-\frac{3}{4}\end{cases}}\)
28 tháng 6 2021
b) Ta có: \(\sin^2\alpha+\cos^2\alpha=1\)
\(\Leftrightarrow\cos^2\alpha=\dfrac{16}{25}\)
hay \(\cos\alpha=\dfrac{4}{5}\)
Ta có: \(A=5\cdot\sin^2\alpha+6\cdot\cos^2\alpha\)
\(=5\cdot\left(\dfrac{3}{5}\right)^2+6\cdot\left(\dfrac{4}{5}\right)^2\)
\(=5\cdot\dfrac{9}{25}+6\cdot\dfrac{16}{25}\)
\(=\dfrac{141}{25}\)
c) Ta có: \(\tan\alpha=\dfrac{1}{\cot\alpha}=\dfrac{1}{\dfrac{4}{3}}=\dfrac{3}{4}\)
\(D=\dfrac{\sin\alpha+\cos\alpha}{\sin\alpha-\cos\alpha}\)
\(=\dfrac{\dfrac{9}{16}+\dfrac{16}{9}}{\dfrac{9}{16}-\dfrac{16}{9}}=-\dfrac{337}{175}\)
15 tháng 7 2017
ta co \(sin^2a+cos^2a=1\Rightarrow cosa=0.36\)
\(\frac{sina}{cosa}=tana\Rightarrow tana=\frac{20}{9}\)
\(tana\cdot cotga=1\Rightarrow cotga=\frac{9}{20}\)
câu b tương tự nha cau c \(\frac{sina+cosa}{sina-cosa}=\) bn
6 tháng 10 2021
Bài 1:
\(\cos\alpha=\dfrac{4}{5}\)
\(\tan\alpha=\dfrac{3}{4}\)
\(\cot\alpha=\dfrac{4}{3}\)
a) \(\sin\alpha=\sqrt{1-\cos^2\alpha}=0.6\)
\(\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{0.6}{0.8}=\dfrac{3}{4}\)
\(\cot\alpha=\dfrac{1}{\tan\alpha}=\dfrac{4}{3}\)