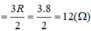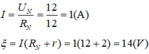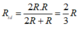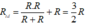Có các điện trở R với giá trị như nhau được mắc theo sơ đồ như sau
- Các điện trở được mắc nối tiếp thành một dãy gồm A điện trở, gọi là một “cụm”.
- Các cụm y hệt này được mắc song song với nhau thành một hàng B dãy.
Hãy tính các giá trị sau theo A và B: điện trở tương đương, công suất tỏa nhiệt trên mỗi điên trở, mỗi cụm, và
trên toàn mạch khi cả hệ thống được mắc vào nguồn có hiệu điện thế Uo. Biết rằng các dây dẫn và nguồn là lý
tưởng và các số A;B là số tự nhiên.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
\(R_{12}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{100.100}{100+100}=50\left(\Omega\right)\)
Điện trở toàn mạch là:
\(R_{tđ}=R_{23}+R_3=50+50=100\left(\Omega\right)\)
Bài 2:
Ta có: \(R_{tđ}=R_1+R_2+R_3=150\left(\Omega\right)\)
Mà \(R_1=R_2=R_3\)
\(\Rightarrow R_1=R_2=R_3=150:3=50\left(\Omega\right)\)
Bài 3:
Điện trở dây dẫn là:
\(R=\dfrac{U}{I}=\dfrac{18}{2,5}=7,2\left(\Omega\right)\)

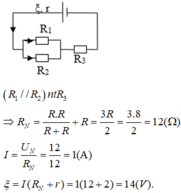
Theo sơ đồ Hình 10.6a và nếu R = r thì dòng điện chạy qua R có cường độ là:
![]()
Theo sơ đồ Hình 10.6b và nếu R = r thì dòng điện chạy qua R có cường độ là:
![]()
Từ (1) và (2) cho ta điều phải chứng minh

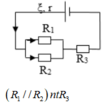
+ Cách mắc 1 : Ta có (( R0 // R0 ) nt R0 ) nt r \(\Rightarrow\) (( R1 // R2 ) nt R3 ) nt r đặt R1 = R2 = R3 = R0
Dòng điện qua R3 : I3 = \(I_3=\frac{U}{R+R_0+\frac{R_0}{2}}=\frac{0,8R_0}{2,5R_0}=0,32A\). Do R1 = R2 nên I1 = I2 = \(\frac{I_3}{2}=0,6A\)
+ Cách mắc 2 : Cường độ dòng điện trong mạch chính I’ = \(\frac{U}{r+\frac{2R_0.R_0}{3R_0}}=\frac{0,8R_0}{\frac{5R_0}{3}}=0,48A\).
Hiệu điện thế giữa hai đầu mạch nối tiếp gồm 2 điện trở R0 : U1 = I’. \(\frac{2R_0.R_0}{3R_0}=0,32R_0\)
\(\Rightarrow\) cường độ dòng điện qua mạch nối tiếp này là I1 = \(\frac{U_1}{2R_0}=\frac{0,32R_0}{2R_0}=0,16A\) \(\Rightarrow\) CĐDĐ qua điện trở còn lại là I2 = 0,32A.
b/ Ta nhận thấy U không đổi \(\Rightarrow\) công suất tiêu thụ ở mạch ngoài P = U.I sẽ nhỏ nhất khi I trong mạch chính nhỏ nhất \(\Rightarrow\) cách mắc 1 sẽ tiêu thụ công suất nhỏ nhất và cách mắc 2 sẽ tiêu thụ công suất lớn nhất.