cho tam giác ABC cân ở A có M,N lần lượt là trung điểm của BC và AC . đường thẳng MN cắt đường thẳng song song với BC kẻ từ A tại D
a, chứng minh ABMD là hình bình hành
b, so sánh MD với AC
c, tứ giác ADCM là hình đặc biệt nào? vì sao
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 10 2019
bài 1 . c) dễ dàng chứng minh tam giác DMA = tam giác DME (2 cạnh góc vuông) .Ta đc DA=DE , mà AD =BC nên BC = DC
Suy ra : tam giác AME = tam giác NBC ( cạnh huyền-cạnh góc vuông ) .( 1)
Tam giác MAN và tam giác EMC có : AN song song với MC nên góc EMC = góc MAN mà AN=MC(ANCM là hbh) , ME=MA nên 2 tam giác này bằng nhau (c.g.c) ;Suy ra góc M= góc e suy ra EC// MN (2)
Từ (1) và (2) suy ra là htc
23 tháng 10 2019
caau1 d) dựa vào tính chất 2 đường chéo = nhau song chứng minh từ từ là ra bởi đã có góc E=C= 90 độ
5 tháng 3 2022
Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC
hay BMNC là hình thang
b: Xét ΔABK có MI//BK
nên MI/BK=AM/AB=1/2(1)
XétΔACK có NI//CK
nên NI/CK=AN/AC=1/2(2)
Từ (1)và (2) suy ra MI/BK=NI/CK
mà MI=NI
nên BK=CK
hay K là trug điểm của BC
Xét ΔABC có
K là trung điểm của BC
M là trung điểm của AB
Do đó: KM là đường trung bình
=>KM//AN và KM=AN
hay AMKN là hình bình hành
5 tháng 11 2017
a) gócm=gócb =gócc=gócn mn // bc
b) ncf=cne=anm=gócb=cfe=fen; tam giác ine=tam giác icf suy ra ne=cf
c) suy ra necf là hình bình hành có fe=in+nc=ie+if =nc nên necf là hcn
CM
4 tháng 1 2017
a) Xét tứ giác ADME có:
∠(DAE) = ∠(ADM) = ∠(AEM) = 90o
⇒ Tứ giác ADME là hình chữ nhật (có ba góc vuông).
b) Ta có ME // AB ( cùng vuông góc AC)
M là trung điểm của BC (gt)
⇒ E là trung điểm của AC.
Ta có E là trung điểm của AC (cmt)
Chứng minh tương tự ta có D là trung điểm của AB
Do đó DE là đường trung bình của ΔABC
⇒ DE // BC và DE = BC/2 hay DE // MC và DE = MC
⇒ Tứ giác CMDE là hình bình hành.
c) Ta có DE // HM (cmt) ⇒ MHDE là hình thang (1)
Lại có HE = AC/2 (tính chất đường trung tuyến của tam giác vuông AHC)
DM = AC/2 (DM là đường trung bình của ΔABC) ⇒ HE = DM (2)
Từ (1) và (2) ⇒ MHDE là hình thang cân.
d) Gọi I là giao điểm của AH và DE. Xét ΔAHB có D là trung điểm của AB, DI // BH (cmt) ⇒ I là trung điểm của AH
Xét ΔDIH và ΔKIA có
IH = IA
∠DIH = ∠AIK (đối đỉnh),
∠H1 = ∠A1(so le trong)
ΔDIH = ΔKIA (g.c.g)
⇒ ID = IK
Tứ giác ADHK có ID = IK, IA = IH (cmt) ⇒ DHK là hình bình hành
⇒ HK // DA mà DA ⊥ AC ⇒ HK ⊥ AC
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
20 tháng 9 2023
a/
Ta có
FA=FC; GB=GC => GF là đường trung bình của tg ABC
=> GF//AB Mà \(AB\perp AC\)
\(\Rightarrow GF\perp AC\)
=> AEGF là hình thang vuông tại A và F
b/
EI//BF (gt)
GF//AB => FI//BE
=> BEIF là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
c/
Ta có GF là đường trung bình của tg ABC \(\Rightarrow GF=\dfrac{1}{2}AB\)
BEIF là hbh (cmt) =>FI=EB
Mà \(EA=EB=\dfrac{1}{2}AB\)
=> GF=FI
Ta có
FA=FC
=> AGCI là hình bình hành (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
Mà \(GF\perp AC\Rightarrow GI\perp AC\)
=> AGCI là hình thoi (Hình bình hành có 2 đường chéo vuông góc là hình thoi)
d/
Để AGCI là hình vuông \(\Rightarrow AG\perp BC\) => AG là đường cao của tg ABC
Mà GB=GC => AG là đường trung tuyến của tg ABC
=> tg ABC là tg cân tại A (Tam giác có đường cao và đồng thời là đường trung tuyến là tg cân)
Mà \(\widehat{A}=90^o\) (gt)
=> Đk để AGCI là hình vuông thì tg ABC phải là tg vuông cân tại A
KV
16 tháng 12 2023
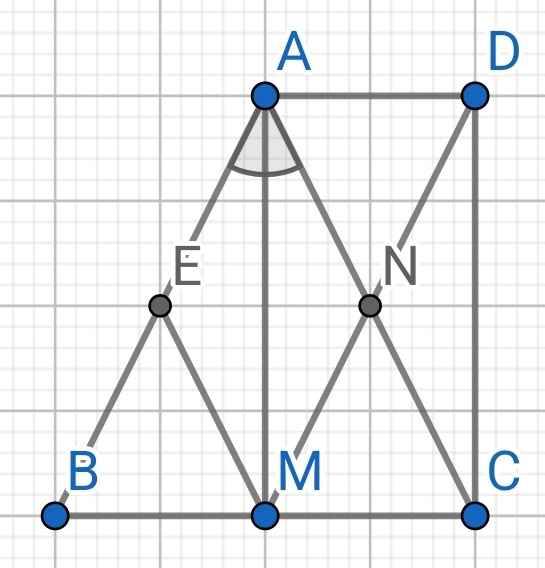a) Do MN // AB (gt)
⇒ MN // AE
Do ME // AC (gt)
⇒ ME // AN
Do AM là tia phân giác của ∠BAC (gt)
⇒ AM là tia phân giác của ∠EAN
Xét tứ giác AEMN có:
MN // AE (cmt)
ME // AN (cmt)
⇒ AEMN là hình bình hành
Mà AM là tia phân giác của ∠EAN (cmt)
⇒ AEMN là hình thoi
b) Do D là điểm đối xứng của M qua N (gt)
⇒ N là trung điểm của DM
∆ABC cân tại A có AM là tia phân giác của ∠BAC (gt)
⇒ AM cũng là đường trung trực của ∆ABC
⇒ M là trung điểm của BC
∆ABC có:
M là trung điểm của BC (cmt)
MN // AB (gt)
⇒ N là trung điểm của AC
Tứ giác ADCM có:
N là trung điểm của DM (cmt)
N là trung điểm của AC (cmt)
⇒ ADCM là hình bình hành
⇒ AD // CM
⇒ AD // BM
Do MN // AB (gt)
⇒ MD // AB
Tứ giác ADMB có:
MD // AB (cmt)
AD // BM (cmt)
⇒ ADMB là hình bình hành
a: Xét ΔABC có
M là trung điểm của BC
N là trung điểm của AC
DO đó: MN là đường trung bình
=>MN//AB
hay MD//AB
Xét tứ giác ABMD có
AD//BM
AB//MD
Do đó; ABMD là hình bình hành
b:
Ta có: MN=1/2AB
nên MN=1/2AC
mà MN=1/2MD
nên AC=MD
c: Ta có: ABMD là hình bình hành
nên AD//MB và AD=MB
=>AD//MC và AD=MC
Xét tứ giác AMCD có
AD//MC
AD=MC
Do đó: AMCD là hình bình hành
mà MD=AC
nên AMCD là hình chữ nhật