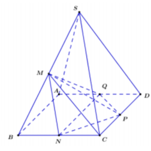
cho hình chóp SABCD có đáy ABCD là hình bình hành .M;N lần lượt là trung điểm của SB và CD
1.Tìm giao tuyến của 2 mặt phẳng (SAD) và (SBC)
2. Chứng minh MN // (SAD)
3.xác định giao điểm I của MN và (SAC) .tính tỉ số IM/ IN
giúp mình với ạ!!!!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 7 2021
Trong mp (ABCD), nối MN kéo dài lần lượt cắt AD tại F và DC tại G
Trong mp (SAD), nối FE cắt SA tại P
Trong mp (SCD), nối EG cắt SC tại Q
\(\Rightarrow\) Ngũ giác MNQEP là thiết diện của (MNE) và chóp
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 12 2020
Trong tam giác SBD, MN là đường trung bình \(\Rightarrow MN||BD\)
\(\Rightarrow MN||\left(ABCD\right)\)
Trong mp (ABCD), qua E kẻ đường thẳng song song BD cắt BC tại F và cắt AD kéo dài tại G
Trong mp (SAD), nối GN kéo dài cắt SA tại P
Ngũ giác PNEFM là thiết diện của (MNE) và chóp
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 12 2020
Trong mp (ABCD), nối AN kéo dài cắt BC kéo dài tại E
\(\Rightarrow E\in\left(SBC\right)\)
Do AD song song BE, áp dụng Talet:
\(\dfrac{AN}{NE}=\dfrac{ND}{NC}=1\Rightarrow AN=NE\Rightarrow\) N là trung điểm AE
\(\Rightarrow MN\) là đường trung bình tam giác SAE
\(\Rightarrow MN//SE\Rightarrow MN//\left(SBC\right)\)
CM
24 tháng 9 2017
Phương pháp:
Công thức tính thể tích khối chóp có diện tích đáy S và chiều cao h là: V = 1 3 S h
Cách giải:
