có 2 số tự nhiên nào mà hiệu của chúng = 98 và tích = 2018 hay không?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




b: Gọi số bị trừ là x
Số trừ là x-98
Theo đề, ta có: \(x\left(x-98\right)=1998\)
\(\Leftrightarrow x^2-98x-1998=0\)
mà x nguyên
nên \(x\notin\varnothing\)

a, Do tổng 2 số đó là lẻ nên trong 2 số đó có 1 số chẵn, 1 số lẻ => tích của chúng là chẵn, không thể = 5749
Vậy không tồn tại 2 số tự nhiên nào thỏa mãn đề bài
b, Do hiệu 2 số đó là 2002 => 2 số đó cùng chẵn hoặc cùng lẻ
Mà tích của chúng là chẵn => 2 số đó cùng chẵn
=> tích của chúng chia hết cho 4, mà 2006 kkhông chia hết cho 4
Vậy không tồn tại 2 số tự nhiên nào thỏa mãn đề bài
a, Do tổng 2 số đó là lẻ nên trong 2 số đó có 1 số chẵn, 1 số lẻ => tích của chúng là chẵn, không thể = 5749
Vậy không tồn tại 2 số tự nhiên nào thỏa mãn đề bài
b, Do hiệu 2 số đó là 2002 => 2 số đó cùng chẵn hoặc cùng lẻ
Mà tích của chúng là chẵn => 2 số đó cùng chẵn
=> tích của chúng chia hết cho 4, mà 2006 kkhông chia hết cho 4
Vậy không tồn tại 2 số tự nhiên nào thỏa mãn đề bài


Gọi 2 số tự nhiên đó lần lượt là a và b \(\left(a,b\in N\text{*}\right)\)
Theo đề ta có:
\(\begin{cases}a-b=2016\left(1\right)\\ab=20162018\left(2\right)\end{cases}\)\(\left(1\right)\Leftrightarrow a=2016+b\)
Thay vào (2) ta có:
\(\left(2016+b\right)b=20162018\)
Bấm máy ta có không có a,b nào thỏa mãn
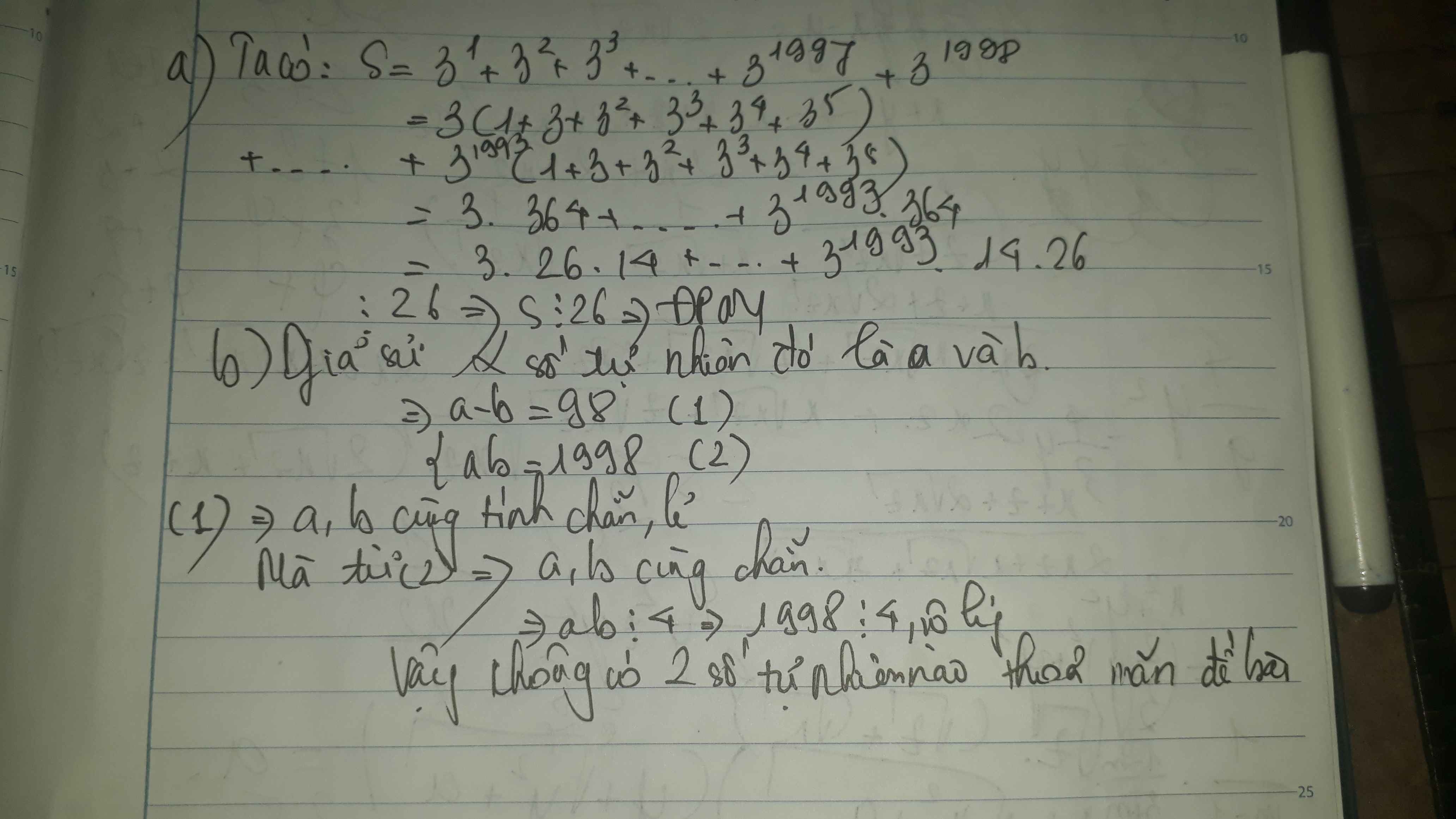
Gọi số tự nhiên đó lần lượt là a,b
Theo đề ta có:
\(\begin{cases}a-b=98\left(1\right)\\ab=2018\left(2\right)\end{cases}\)
\(\left(1\right)\Rightarrow a=98+b\). Thay vào (2) ta có:
\(\left(2\right)\Rightarrow\left(b+98\right)b=2018\)
\(\Rightarrow b^2+98b=2018\)
\(\Rightarrow b^2+98b-2018=0\)
Bấm máy tính ta không nhận được giá trị a,b tự nhiên thỏa mãn