Giúp minh vơi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
HT
2

15 tháng 12 2021
a. Chu vi là \(\left(12+5\right).2=34\left(m\right)\)
Diện tích là \(12.5=60\left(m^2\right)=600000\left(cm^2\right)\)
b. Cần lát \(600000:\left(40.40\right)=375\) viên gạch
BH
12

17 tháng 3 2022
TL:
Sai nhé bạn
Bạn k cho mik cái đi nhé
@@@@@@@@@@@@@@@@@
HT
HT
12
HM
5

HT
5

IO
13 tháng 12 2021
3x . 2 + 15 = 33
3x . 2 = 33 - 15 = 18
3x = 18 : 2 = 9 = 32
=> x = 2

T
13




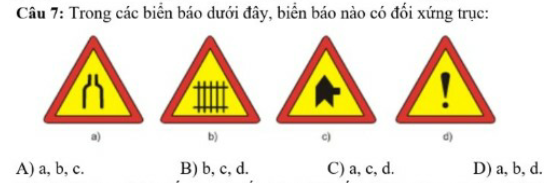
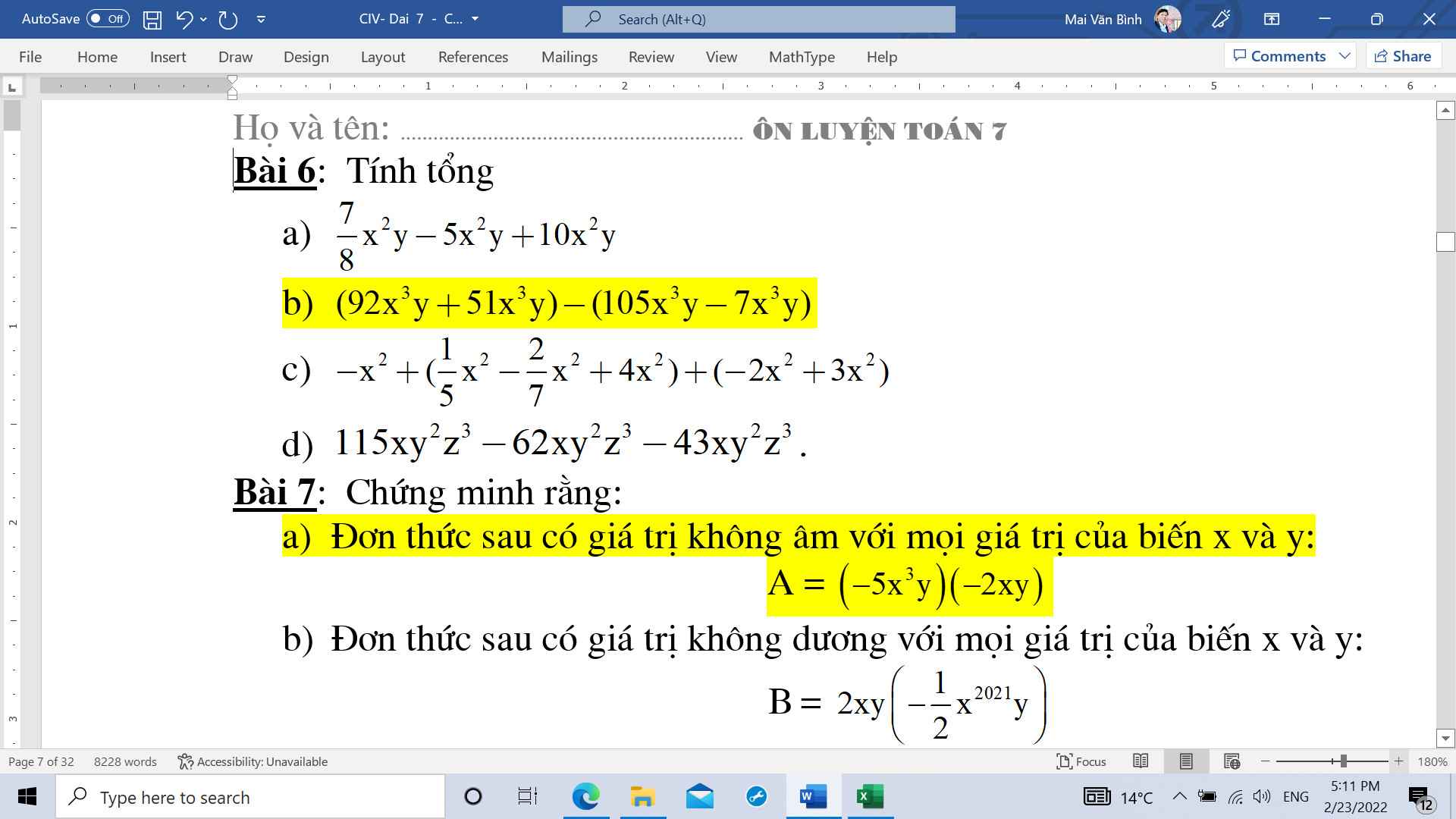
 Ai giúp mình với ạ
Ai giúp mình với ạ
a) C
b) A
c) D
d) D
a)C c)D
b)A d)D