 lm giúp mik vs
lm giúp mik vs
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(M=\sqrt{\dfrac{4}{\left(2-\sqrt{5}\right)^2}}-\sqrt{\dfrac{4}{\left(2+\sqrt{5}\right)^2}}=\dfrac{2}{\left|2-\sqrt{5}\right|}-\dfrac{2}{\left|2+\sqrt{5}\right|}\)
\(=\dfrac{2}{\sqrt{5}-2}-\dfrac{2}{\sqrt{5}+2}=\dfrac{2\left(\sqrt{5}+2\right)-2\left(\sqrt{5}-2\right)}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}\)
\(=\dfrac{8}{1}=8\)
Lm ơn giúp mik đii mà mik bt ơn bn đó nhiều lắm . Mik đang rất cần

2:
a: BC=căn 15^2+20^2=25cm
AH=15*20/25=12cm
góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
=>DE=AH=12cm
b: ΔAHB vuông tại H có HD vuông góc AB
nên AD*AB=AH^2
ΔAHC vuông tại H có HE vuông góc AC
nên AE*AC=AH^2
=>AD*AB=AE*AC
c: góc IAC+góc AED
=góc ICA+góc AHD
=góc ACB+góc ABC=90 độ
=>AI vuông góc ED
4:
a: góc BDH=góc BEH=góc DBE=90 độ
=>BDHE là hình chữ nhật
b: BDHE là hình chữ nhật
=>góc BED=góc BHD=góc A
Xét ΔBED và ΔBAC có
góc BED=góc A
góc EBD chung
=>ΔBED đồng dạng với ΔBAC
=>BE/BA=BD/BC
=>BE*BC=BA*BD
c: góc MBC+góc BED
=góc C+góc BHD
=góc C+góc A=90 độ
=>BM vuông góc ED


a: \(2x^2\left(3xy+x^2-2y^2\right)\)
\(=6x^3y+2x^4-4x^2y^2\)
b: \(\dfrac{1}{3}x^2y^3\left(2x-3y+1\right)\)
\(=\dfrac{2}{3}x^3y^3-x^2y^4+\dfrac{1}{3}x^2y^3\)
h: \(\left(x-1\right)\left(x+1\right)\left(2x-3\right)\)
\(=\left(x^2-1\right)\left(2x-3\right)\)
\(=2x^3-3x^2-2x+3\)


Bài 1:
a) \(5x^2y-10xy^2=5xy\left(x-y\right)\)
b) \(4x\left(2y-z\right)+7y\left(z-2y\right)=\left(4x-7y\right)\left(2y-z\right)\)
c) \(5x^2y^3-25x^3y^4+10x^3y^3=5x^2y^3\left(1-5xy+2x\right)\)
d) \(12x^2y-18xy^2-30y^2=6y\left(2x^2-3xy-5y\right)\)
e) \(y\left(a-b\right)-7y^2\left(b-a\right)=\left(y+7y^2\right)\left(a-b\right)\)
f) \(27x^2\left(y-1\right)-9x^3\left(1-y\right)=\left(27x^2+9x^3\right)\left(y-1\right)=9x^2\left(3+x\right)\left(y-1\right)\)

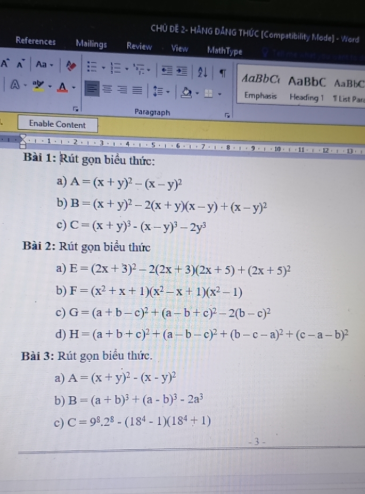
bài 1
a)
=(x+y-x+y)(x+y+x-y)
=2x.2y
=4xy
b)
B=(x+y-x+y)2=4y2
c)
=(x+y-x+y)[(x+y)2+(x+y)(x-y)+(x-y)2]-2y3
=2y(\(x^2+2xy+y^2+x^2-y^2+x^2-2xy+y^2\))-2y3
=\(2y\left(3x^2+y^2\right)-2y^3=6x^2y+2y^3-2y^3=6x^2y\)
Bài 3:
a: Ta có: \(A=\left(x+y\right)^2-\left(x-y\right)^2\)
\(=x^2+2xy+y^2-x^2+2xy-y^2\)
=4xy
b: ta có: \(B=\left(a+b\right)^3+\left(a-b\right)^3-2a^3\)
\(=a^3+3a^2b+3ab^2+b^3+a^3-3a^2b+3ab^2-b^3-2a^3\)
\(=6ab^2\)
c: Ta có: \(C=9^8\cdot2^8-\left(18^4-1\right)\left(18^4+1\right)\)
\(=18^8-18^8+1\)
=1








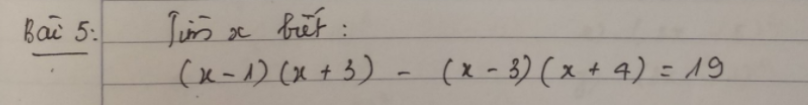

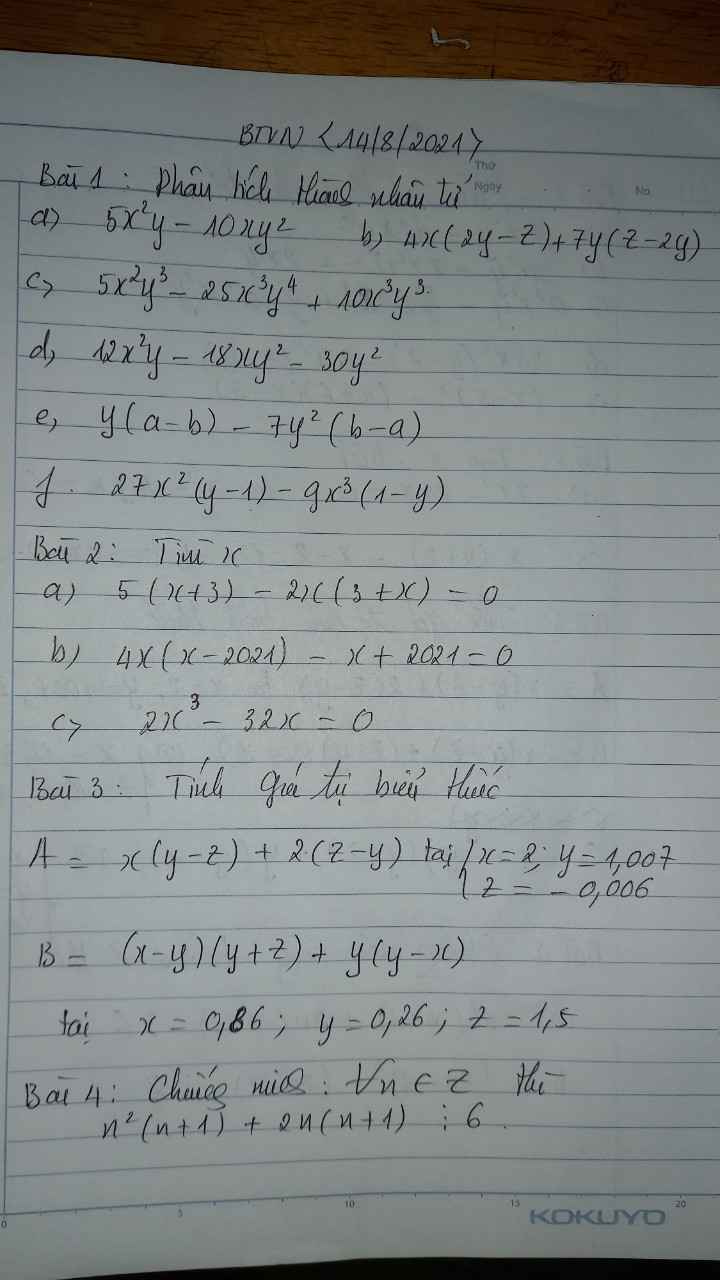 lm giúp mik vs
lm giúp mik vs 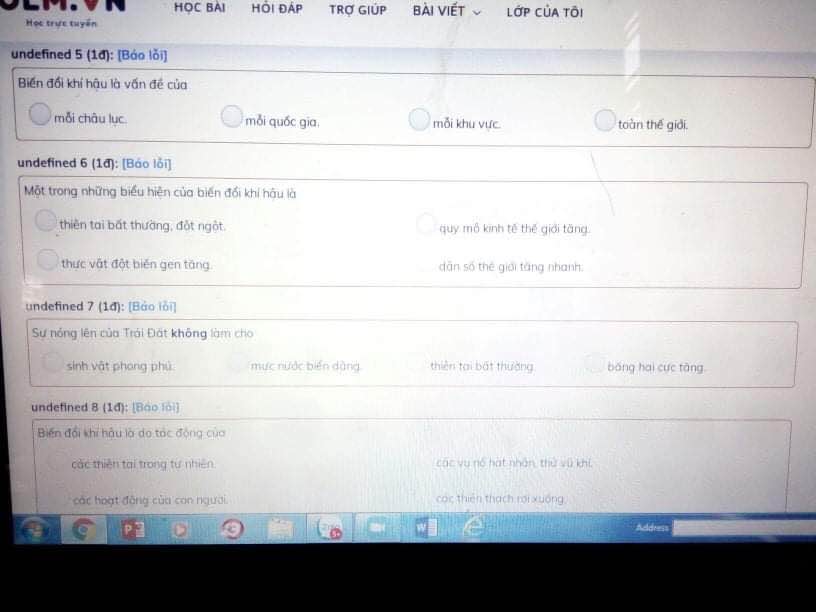
 lm giúp mik vs
lm giúp mik vs
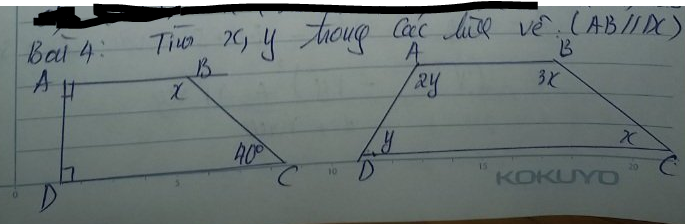
Hình 1: x = 140
Hình 2: x = 90
y = 120