Tìm GTNN của 2x2 - 5x + 13
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 10 2021
a) \(4x^2+12x+1=\left(4x^2+12x+9\right)-8=\left(2x+3\right)^2-8\ge-8\)
\(ĐTXR\Leftrightarrow x=-\dfrac{3}{2}\)
b) \(4x^2-3x+10=\left(4x^2-3x+\dfrac{9}{16}\right)+\dfrac{151}{16}=\left(2x-\dfrac{3}{4}\right)^2+\dfrac{151}{16}\ge\dfrac{151}{16}\)
\(ĐTXR\Leftrightarrow x=\dfrac{3}{8}\)
c) \(2x^2+5x+10=\left(2x^2+5x+\dfrac{25}{8}\right)+\dfrac{55}{8}=\left(\sqrt{2}x+\dfrac{5\sqrt{2}}{4}\right)^2+\dfrac{55}{8}\ge\dfrac{55}{8}\)
\(ĐTXR\Leftrightarrow x=-\dfrac{5}{4}\)
d) \(x-x^2+2=-\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{9}{4}=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{9}{4}\le\dfrac{9}{4}\)
\(ĐTXR\Leftrightarrow x=\dfrac{1}{2}\)
e) \(2x-2x^2=-2\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{1}{2}=-2\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{2}\le\dfrac{1}{2}\)
\(ĐTXR\Leftrightarrow x=\dfrac{1}{2}\)
f) \(4x^2+2y^2+4xy+4y+5=\left(4x^2+4xy+y^2\right)+\left(y^2+4y+4\right)+1=\left(2x+y\right)^2+\left(y+2\right)^2+1\ge1\)
\(ĐTXR\Leftrightarrow\) \(\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
4 tháng 10 2021
a: Ta có: \(4x^2+12x+1\)
\(=4x^2+12x+9-8\)
\(=\left(2x+3\right)^2-8\ge-8\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{3}{2}\)
b: Ta có: \(4x^2-3x+10\)
\(=4\left(x^2-\dfrac{3}{4}x+\dfrac{5}{2}\right)\)
\(=4\left(x^2-2\cdot x\cdot\dfrac{3}{8}+\dfrac{9}{64}+\dfrac{151}{64}\right)\)
\(=4\left(x-\dfrac{3}{8}\right)^2+\dfrac{151}{16}\ge\dfrac{151}{16}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{3}{8}\)
c: Ta có: \(2x^2+5x+10\)
\(=2\left(x^2+\dfrac{5}{2}x+5\right)\)
\(=2\left(x^2+2\cdot x\cdot\dfrac{5}{4}+\dfrac{25}{16}+\dfrac{55}{16}\right)\)
\(=2\left(x+\dfrac{5}{4}\right)^2+\dfrac{55}{8}\ge\dfrac{55}{8}\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{5}{4}\)
MM
3
1 tháng 9 2021
a) \(2x^2-x+1=2\left(x-\dfrac{1}{4}\right)^2+\dfrac{7}{8}\ge\dfrac{7}{8}\)
\(ĐTXR\Leftrightarrow x=\dfrac{1}{4}\)
b) \(5x-x^2+4=-\left(x-\dfrac{5}{2}\right)^2+\dfrac{41}{4}\le\dfrac{41}{4}\)
\(ĐTXR\Leftrightarrow x=\dfrac{5}{2}\)
c) \(x^2+5y^2-2xy+4y+3=\left(x-y\right)^2+\left(2y+1\right)^2+2\ge2\)
\(ĐTXR\Leftrightarrow\)\(x=y=-\dfrac{1}{2}\)
1 tháng 9 2021
b: ta có: \(-x^2+5x+4\)
\(=-\left(x^2-5x-4\right)\)
\(=-\left(x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}-\dfrac{41}{4}\right)\)
\(=-\left(x-\dfrac{5}{2}\right)^2+\dfrac{41}{4}\le\dfrac{41}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{5}{2}\)
KR
7 tháng 5 2018
Áp dụng Bunyakovsky, ta có :
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)
=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)
=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)
Mấy cái kia tương tự
1 tháng 9 2021
a: Ta có: \(A=x^2+3x+4\)
\(=x^2+2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{7}{4}\)
\(=\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{3}{2}\)
16 tháng 9 2023
a) \(2x^2-5x^2+6x+13=0\)
\(\Leftrightarrow-3x^2+6x+13=0\)
\(\Leftrightarrow3x^2-6x-13=0\left(1\right)\)
\(\Delta'=9+39=48>0\Rightarrow\sqrt[]{\Delta'}=4\sqrt[]{3}\)
Pt (1) có 2 nghiệm phân biệt là :
\(\left[{}\begin{matrix}x=\dfrac{3+4\sqrt[]{3}}{3}=1+\dfrac{4\sqrt[]{3}}{3}\\x=\dfrac{3-4\sqrt[]{3}}{3}=1-\dfrac{4\sqrt[]{3}}{3}\end{matrix}\right.\)
b) \(x^2-5x=-4\)
\(\Leftrightarrow x^2-5x+4=0\)
\(\Leftrightarrow x^2-x-4x+4=0\)
\(\Leftrightarrow x\left(x-1\right)-4\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=4\end{matrix}\right.\)
22 tháng 7 2023
Sửa đề: tìm GTLN
E=-2(x^2+3/2x-5/2)
=-2(x^2+2*x*3/4+9/16-49/16)
=-2(x+3/4)^2+49/8<=49/8
Dấu = xảy ra khi x=-3/4
CM
16 tháng 12 2019
Giá trị của biểu thức xác định khi mỗi giá trị của phân thức trong biểu thức đều được xác định.
Khi đó điều kiện xác định:
CM
5 tháng 9 2019
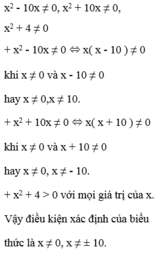
Giá trị của biểu thức xác định khi mỗi giá trị của phân thức trong biểu thức đều được xác định.
Khi đó điều kiện xác định:
2x^2-5x+13
=2*[x^2-(5/2)x+13/2]
=2*[x^2-2x(5/4)+25/16+79/16]
=2*(x-5/4)^2+79/8
vì 2*(x-5/4)^2>=0 (với mọi x) suy ra 2*(x-5/4)^2+79/8>=79/8 (với mọi x)
Vậy GTNN là 79/8
Bấm máy tính là ra hết á mà