Câu4: Giải phương trình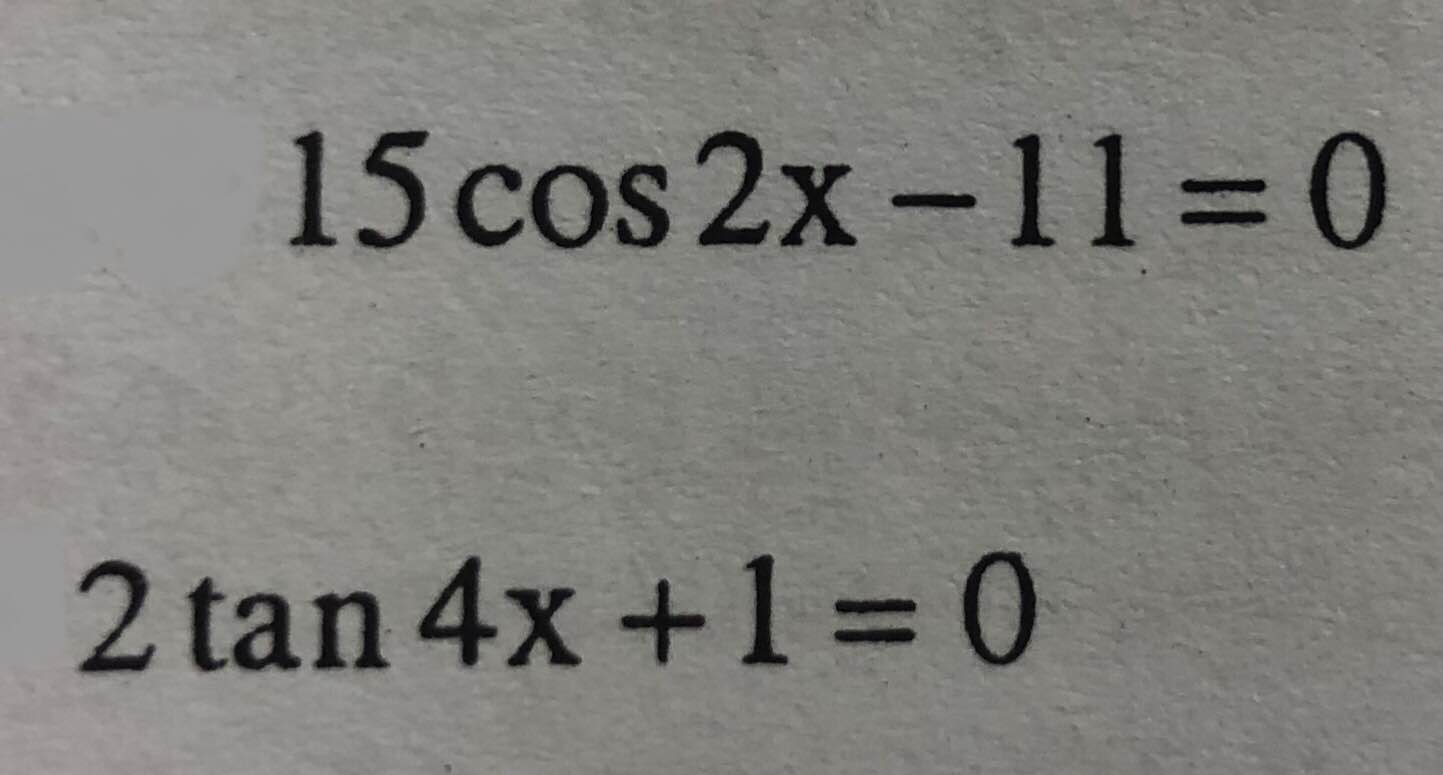
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TP
11 tháng 5 2022
- Tính toán:
+ Khối lượng NaCl cần dùng để pha chế 500g dung dịch nước muối sinh lý NaCl 0,9% là:
\(m_{NaCl}=500.0,9\%=4,5\left(g\right)\)
+ Khối lượng nước cất cần dùng là
\(m_{H_2O}=500-4,5=495,5\left(g\right)\)
- Tiến hành
+ Cân lấy 4,5g NaCl cho vào cốc thủy tinh có dung tích lớn hơn 500ml
+ Cân lấy 495,5g nước cất, sau đó cho tiếp vào cốc thủy tinh đựng NaCl. Khuấy đều cho NaCl tan hết, ta thu được 500g dung dịch nước muối sinh lý NaCl 0,9%
TP
30 tháng 11 2021
\(a.Mg+2HCl\rightarrow MgCl_2+H_2\\ n_{H_2}=\dfrac{44,8}{22,4}=2\left(mol\right)\\ n_{HCl}=2n_{H_2}=4\left(mol\right)\\ \Rightarrow m_{HCl}=4.36,5=146\left(g\right)\\ c.n_{MgCl_2}=n_{H_2}=2\left(mol\right)\\ \Rightarrow m_{MgCl_2}=2.95=190\left(g\right)\)
DV
3
15 tháng 12 2023
a: Để đồ thị hàm số (1) song song với đường thẳng y=3x+1 thì
\(\left\{{}\begin{matrix}m-1=3\\2m-5\ne1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=4\\2m\ne6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=4\\m\ne3\end{matrix}\right.\)
=>m=4
b: Thay m=1,5 vào (1), ta được:
\(y=\left(1,5-1\right)x+2\cdot1,5-5=0,5x-2\)
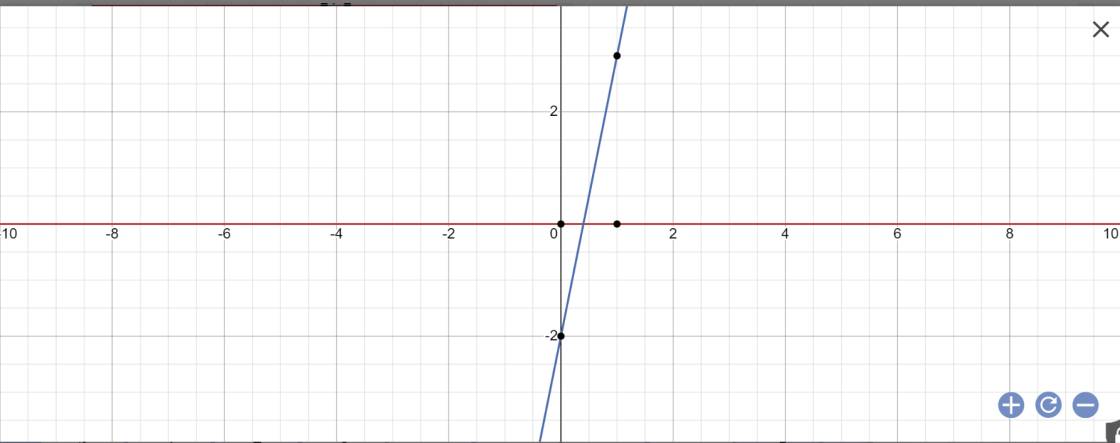
Gọi \(\alpha\) là góc tạo bởi (1) với trục Ox
y=0,5x-2 nên a=0,5
\(tan\alpha=a=0,5\)
=>\(\alpha\simeq26^034'\)
NM
Nguyễn Minh Quang
Giáo viên
5 tháng 3 2022
ta có :
\(\left|x+1\right|+\left|x-1\right|=1+\left|\left(x-1\right)\left(x+1\right)\right|\)
\(\Leftrightarrow\left|x-1\right|\left|x+1\right|-\left|x-1\right|-\left|x+1\right|+1=0\)
\(\Leftrightarrow\left(\left|x-1\right|-1\right)\left(\left|x+1\right|-1\right)=0\Leftrightarrow\orbr{\begin{cases}\left|x-1\right|=1\\\left|x+1\right|=1\end{cases}}\)
\(\Leftrightarrow x\in\left\{-2,0,2\right\}\)
15cos2x-11=0
⇔ cos2x=\(\dfrac{11}{15}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=15+k2\pi\\2x=-15+k2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{15}{2}+k\pi\\x=\dfrac{-15}{2}+k\pi\end{matrix}\right.\)
a.
\(15cos2x-11=0\)
\(\Leftrightarrow cos2x=\dfrac{11}{15}\)
\(\Leftrightarrow2x=\pm arccos\left(\dfrac{11}{15}\right)+k2\pi\)
\(\Leftrightarrow x=\pm\dfrac{1}{2}arccos\left(\dfrac{11}{15}\right)+k\pi\)
b.
\(2tan4x+1=0\)
\(\Leftrightarrow tan4x=-\dfrac{1}{2}\)
\(\Leftrightarrow4x=arctan\left(-\dfrac{1}{4}\right)+k\pi\)
\(\Leftrightarrow x=\dfrac{1}{4}arctan\left(-\dfrac{1}{4}\right)+\dfrac{k\pi}{4}\)