K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
2 tháng 11 2017
a) Cách giải các phương trình lượng giác cơ bản:
+ Phương trình sin x = a.
Nếu |a| > 1 ⇒ phương trình vô nghiệm.
Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho sin α = a.
Khi đó phương trình trở thành sin x = sin α
⇒ Phương trình có nghiệm: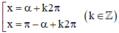 
+ Phương trình cos x = a.
Nếu |a| > 1 ⇒ phương trình vô nghiệm.
Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho cos α = a.
Khi đó phương trình trở thành cos x = cos α.
⇒ Phương trình có nghiệm: x = ±α + k2π (k ∈ Z).
+ Phương trình tan x = a.
Tìm một cung α sao cho tan α = a.
Khi đó phương trình trở thành tan x = tan α.
⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).
+ Phương trình cot x = a
Tìm một cung α sao cho cot α = a.
Khi đó phương trình trở thành cot x = cot α.
⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).
b) Cách giải phương trình a.sin x + b.cos x = c.
+ Nếu a = 0 hoặc b = 0 ⇒ Phương trình lượng giác cơ bản .
+ a ≠ 0 và b ≠ 0. Chia cả hai vế của phương trình cho 
ta được:
Ta giải phương trình trên như phương trình lượng giác cơ bản.
PT
1
PT
1
9D
1
3 tháng 10 2021
\(sinx=\dfrac{2tan\dfrac{x}{2}}{tan^2\dfrac{x}{2}+1}\)
\(cosx=\dfrac{1-tan^2\dfrac{x}{2}}{1+tan^2\dfrac{x}{2}}\)
Đặt \(t=tan\dfrac{x}{2}\)
Khi đó pt: \(\Rightarrow a\cdot\dfrac{2t}{t^2+1}+b\cdot\dfrac{1-t^2}{1+t^2}=c\)
\(\Rightarrow2t\cdot a+\left(1-t^2\right)\cdot b=\left(1+t^2\right)\cdot c\)
11 tháng 9 2021
\(a,f'\left(x\right)=3x^2-6x\\ f'\left(x\right)\le0\Leftrightarrow3x^2-6x\le0\\ \Leftrightarrow3x\left(x-2\right)\le0\Leftrightarrow0\le x\le2\)
AH
Akai Haruma
Giáo viên
11 tháng 9 2021
Lời giải:
a. $f'(x)\leq 0$
$\Leftrightarrow 3x^2-6x\leq 0$
$\Leftrightarrow x(x-2)\leq 0$
$\Leftrightarrow 0\leq x\leq 2$
b.
$f'(x)=x^2-3x+2=0$
$\Leftrightarrow 3x^2-6x=x^2-3x+2=0$
$\Leftrightarrow 3x(x-2)=(x-1)(x-2)=0$
$\Leftrightarrow x-2=0$
$\Leftrightarrow x=2$
c.
$g(x)=f(1-2x)+x^2-x+2022$
$g'(x)=(1-2x)'f(1-2x)'_{1-2x}+2x-1$
$=-2[3(1-2x)^2-6(1-2x)]+2x-1$
$=-24x^2+2x+5$
$g'(x)\geq 0$
$\Leftrightarrow -24x^2+2x+5\geq 0$
$\Leftrightarrow (5-12x)(2x-1)\geq 0$
$\Leftrightarrow \frac{-5}{12}\leq x\leq \frac{1}{2}$
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 8 2021
ĐKXĐ: \(\left\{{}\begin{matrix}cosx\ne0\\cos2x\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{2}+k\pi\\x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\end{matrix}\right.\)
\(\dfrac{3sin2x}{cos2x}-3tanx-\dfrac{5}{2}=0\)
\(\Leftrightarrow\dfrac{6sinx.cosx}{cos^2x-sin^2x}-3tanx-\dfrac{5}{2}=0\)
\(\Rightarrow\dfrac{6tanx}{1-tan^2x}-3tanx-\dfrac{5}{2}=0\)
\(\Rightarrow6tan^3x+5tan^2x+6tanx-5=0\)
\(\Leftrightarrow\left(2tanx-1\right)\left(3tan^2x+4tanx+5\right)=0\)
\(\Leftrightarrow tanx=\dfrac{1}{2}\)
\(\Leftrightarrow x=arctan\left(\dfrac{1}{2}\right)+k\pi\)
3 tháng 8 2021
Pt ⇔\(\dfrac{1}{sinx.cosx}=\dfrac{1}{2sin\left(x+\dfrac{\pi}{3}\right)}\)
⇔ sinx.cosx = 2sin\(\left(x+\dfrac{\pi}{3}\right)\)
⇔ \(\dfrac{1}{2}\)sin2x = 2sin\(\left(x+\dfrac{\pi}{3}\right)\)
⇔ sin2x = 4sin\(\left(x+\dfrac{\pi}{3}\right)\)
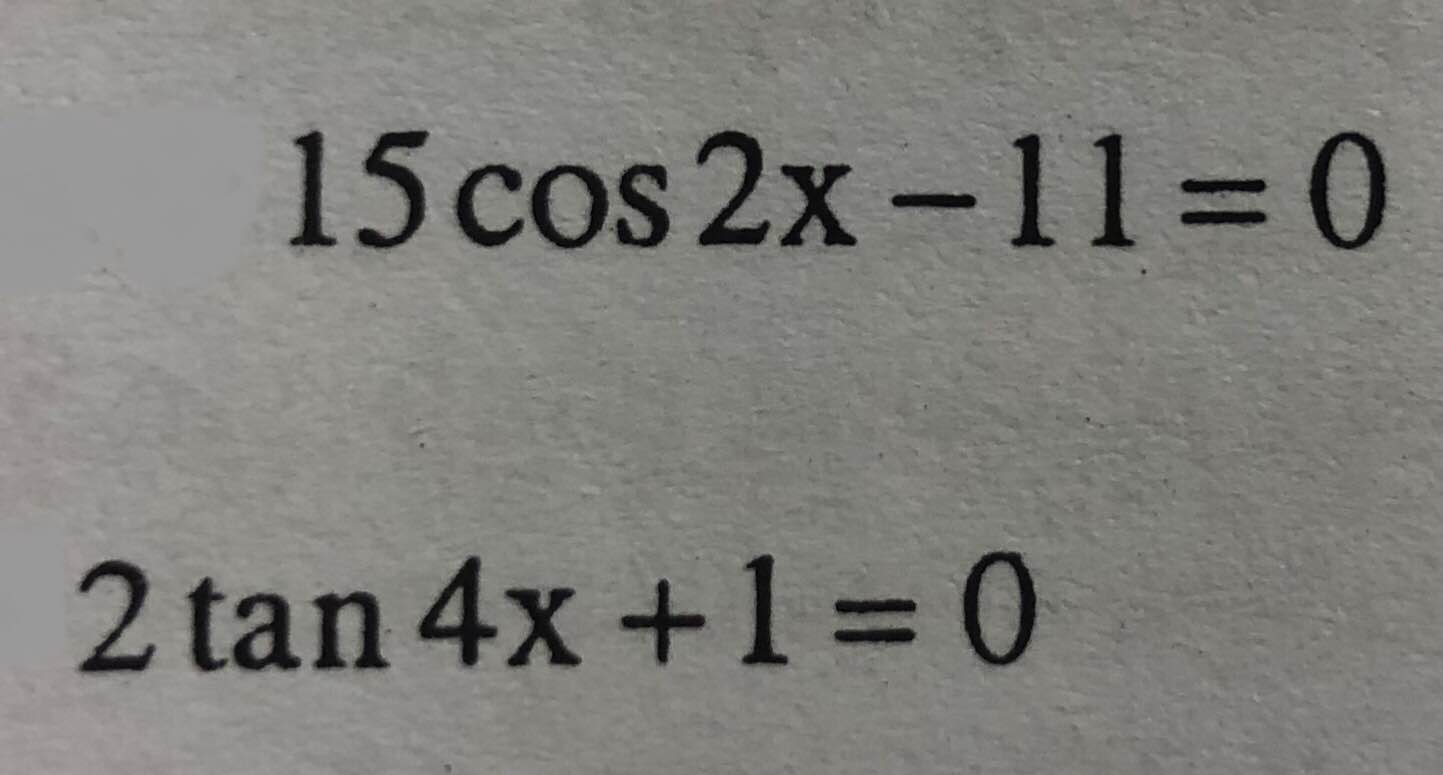
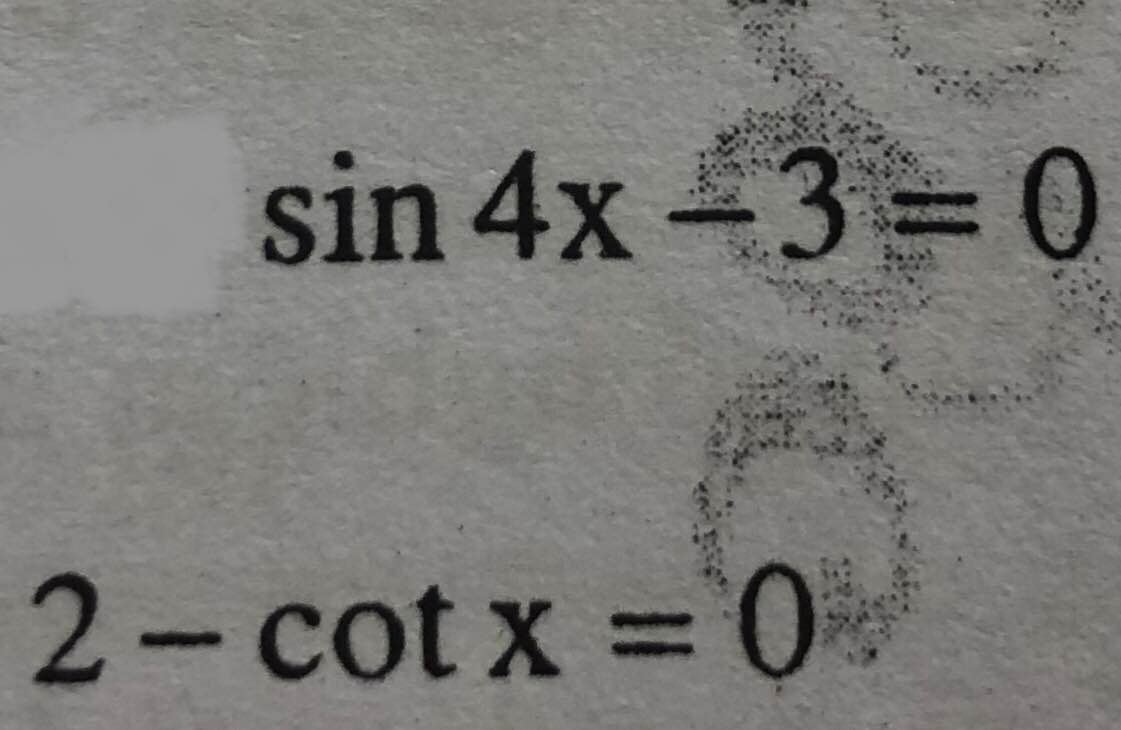
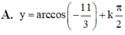
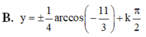
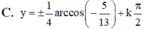
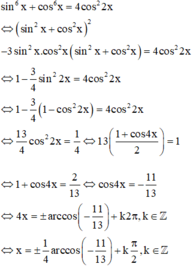
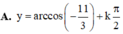
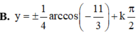
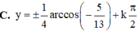
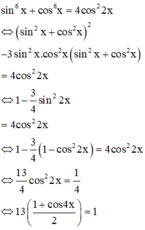
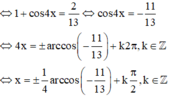
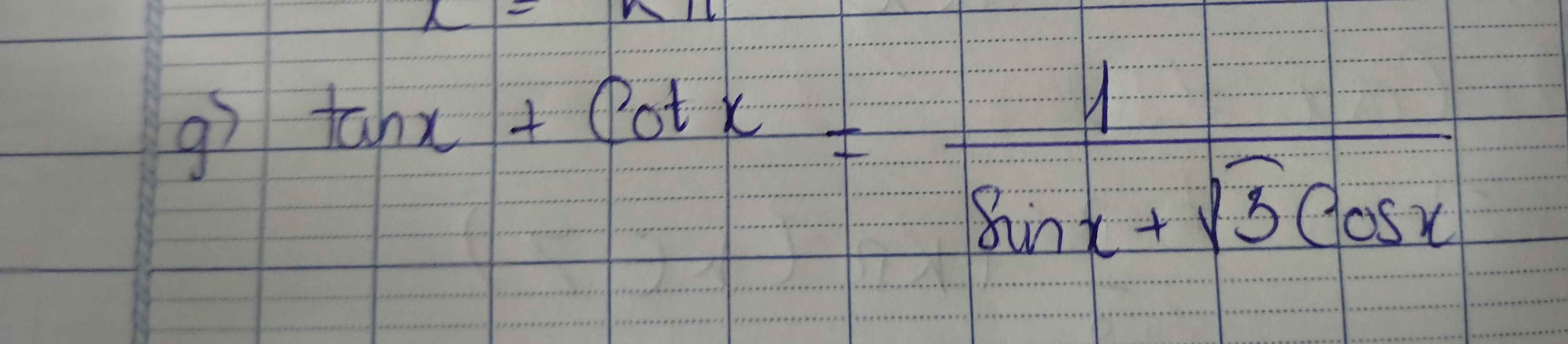
15cos2x-11=0
⇔ cos2x=\(\dfrac{11}{15}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=15+k2\pi\\2x=-15+k2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{15}{2}+k\pi\\x=\dfrac{-15}{2}+k\pi\end{matrix}\right.\)
a.
\(15cos2x-11=0\)
\(\Leftrightarrow cos2x=\dfrac{11}{15}\)
\(\Leftrightarrow2x=\pm arccos\left(\dfrac{11}{15}\right)+k2\pi\)
\(\Leftrightarrow x=\pm\dfrac{1}{2}arccos\left(\dfrac{11}{15}\right)+k\pi\)
b.
\(2tan4x+1=0\)
\(\Leftrightarrow tan4x=-\dfrac{1}{2}\)
\(\Leftrightarrow4x=arctan\left(-\dfrac{1}{4}\right)+k\pi\)
\(\Leftrightarrow x=\dfrac{1}{4}arctan\left(-\dfrac{1}{4}\right)+\dfrac{k\pi}{4}\)