Đặt điện áp \(u = U\sqrt 2\cos \omega t\) (U không đổi, ω thay đổi được) vào hai đầu đoạn mạch gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp. Trên hình vẽ, các đường (1), (2) và (3) là đồ thị của các điện áp hiệu dụng ở hai đầu điện trở \(U_R\), hai đầu tụ điện \(U_C\) và hai đầu cuộn cảm \(U_L\) theo tần số góc ω. Đường...
Đọc tiếp
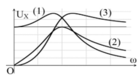
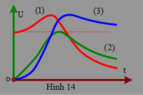
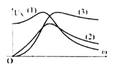
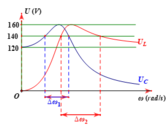
Đặt điện áp \(u = U\sqrt 2\cos \omega t\) (U không đổi, ω thay đổi được) vào hai đầu đoạn mạch gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp. Trên hình vẽ, các đường (1), (2) và (3) là đồ thị của các điện áp hiệu dụng ở hai đầu điện trở \(U_R\), hai đầu tụ điện \(U_C\) và hai đầu cuộn cảm \(U_L\) theo tần số góc ω. Đường (1), (2) và (3) theo thứ tự tương ứng là
A.\(U_C\), \(U_R\) và \(U_L\)
B.\(U_C\), \(U_L\)và \(U_R\)
C.\(U_L\), \(U_R\) và \(U_C\)
D.\(U_R\), \(U_L\) và \(U_C\)
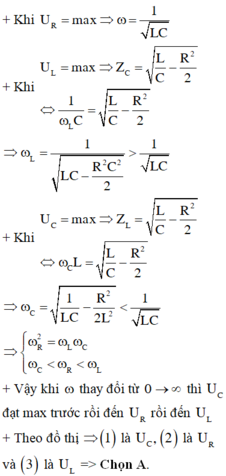
\(U_C=I.Z_C=\dfrac{U.Z_C}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}.\omega C}=\dfrac{U}{\sqrt{\omega^2.C^2.R^2+(\omega^2.LC-1)^2}}\)
Suy ra khi \(\omega=0\) thì \(U_C=U\) \(\Rightarrow (1)\) là \(U_C\)
\(U_L=I.Z_L=\dfrac{U.Z_L}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U.\omega L}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}}=\dfrac{U.L}{\sqrt{\dfrac{R^2}{\omega^2}+(L-\dfrac{1}{\omega^2 C})^2}}\)(chia cả tử và mẫu cho \(\omega\))
Suy ra khi \(\omega\rightarrow \infty\) thì \(U_L\rightarrow U\) \(\Rightarrow (3) \) là \(U_L\)
Vậy chọn \(U_C,U_R,U_L\)