1 chất điểm có khối lượng m=200g, dao đông điều hòa trên trục Ox với cơ năng 0,1J. Trong khoảng thời gian Δt = π/20 s kể từ lúc đầu thì động năng của vật tăng từ 25mJ đến 75mJ. Vật dao động với biên độ là?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


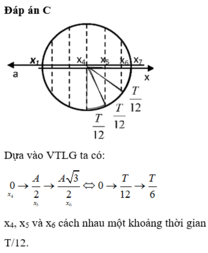
Đáp án C
Thời điểm ban đầu v = v m a x vật đi qua vị trí cân bằng, đến thời điểm t 1 vận tốc giảm một nửa (động năng giảm 4 lần) → t 1 = T 6 = 1 6 s → T = 1 s → ω = 2π rad/s.
Đến thời điểm t 2 = 5 12 s tương ứng với góc quét Δ φ = ω t 2 = 150 0
→ Vật đi được quãng đường s = A + A 2 = 12 cm → A = 8 cm.

Đáp án D
Năng lượng của vật là: ![]()
Tại t=0 thì 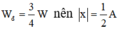
Tại
t
1
thế năng bằng động năng và theo giả thiết
W
đ
tăng đến cực đại rồi giảm, sử dụng đường tròn lượng giác ta được: 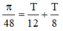 suy ra
suy ra 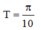 nên
nên ![]()
Mặt khác 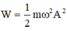 nên A=0,08(m) =8(cm)
nên A=0,08(m) =8(cm)

Đáp án A
Δt là khoảng thời gian giữa hai lần liên tiếp vật có động năng bằng thế năng => ∆ t = T 4
Theo đề bài ta có: ![]()
Công thức độc lập với thời gian giữa gia tốc và vận tốc:
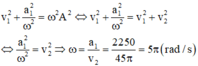
Thay vào công thức tính được biên độ dao động A = 6 3 cm

+ Thời gian hai lần liên tiếp động năng bằng thế năng là ∆ t = T 4 .
+ Vì t1 = t + 0,25T nên v1 vuông pha với v2 → v m a x = v 1 2 + v 2 2 = 16 3 π
+ Áp dụng công thức vuông pha của vận tốc và gia tốc tại thời điểm t ta được:
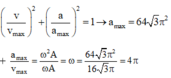
→ A = v m a x ω = 16 π 3 4 π = 4 3 cm
Đáp án C




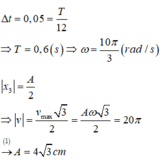
Vận tốc cực đại: \(v_{max}=\sqrt{\dfrac{2W_{đmax}}{m}}=\sqrt{\dfrac{2.0,1}{0,2}}=1m/s\)
Khi \(W_{đ1}=0,025J\) \(\Rightarrow v_{1}=\sqrt{\dfrac{2W_{đ1}}{m}}=\sqrt{\dfrac{2.0,025}{0,2}}=0,5m/s\)
Khi \(W_{đ2}=0,75J\) \(\Rightarrow v_{1}=\sqrt{\dfrac{2W_{đ1}}{m}}=\sqrt{\dfrac{2.0,075}{0,2}}=0,5\sqrt 3m/s\)
Vì vận tốc biến thiên điều hoà theo thời gian, nên ta biểu diễn bằng véc tơ quay:
Từ giản đồ véc tơ ta suy ra được: \(\Delta t=\dfrac{30}{360}T=\dfrac{\pi}{20}\)
\(\Rightarrow T =\dfrac{3\pi}{5}s\)
\(\Rightarrow \omega = \dfrac{2\pi}{T}=\dfrac{10}{3}\) (rad/s)
Biên độ: \(A=\dfrac{v_{max}}{\omega}=0,3m = 30cm\)