Cho tam giác ABC cân tại A, AM là đường trung tuyếna, Chứng minh rằng AM vuông góc BCb, Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh rằng tam giác BMD bằng tam giác CMA. Từ đó suy ra...

NA

Nguyên Anh Phạm

4 tháng 8 2021

Cho tam giác ABC cân tại A, AM là đường trung tuyếna, Chứng minh rằng AM vuông góc BCb, Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh rằng tam giác BMD bằng tam giác CMA. Từ đó suy ra BD = ACc, tính số đo các cạnh tam giác MBD biết AM = 4 cm, BC = 6 cmd, Trên tia đối của tia CB lấy tia lấy điểm E sao cho CB = CE. Chứng minh rằng C là trọng tâm của tam giác...

Đọc tiếp

#Toán lớp 7

0

YN

Yến Ni

4 tháng 5 2022

Cho tam giác ABC cân tại A có AM là đường trung tuyến
a) chứng minh tam giác AMB bằng tam giác AMC
b)trên tia đối của MA lấy điểm D sao cho MA=MD chứng mình BC là tia phân giác của góc ABD
c)lấy điểm E trên đoạn MC sao cho EC =2EM gọi I là trung điểm của DC chứng mình 2EI < AB+CE

#Toán lớp 7

1

E

Etermintrude💫

4 tháng 5 2022

undefined

CHÚC EM HỌC TỐT

Đúng(0)

TP

Tran Phuong Linh

29 tháng 3 2020 - olm

Bài 1: Cho tam giác ABC vuông tại A, AB > AC. M là trung điểm của BC.Trên tia đối của tia MA lấy điểm D sao cho MD = MA.a) Chứng minh rằng: AB = DC và AB // DC.b) Chứng minh rằng:Tam giác ABC=tam giác CDAtừ đó suy ra Am=BC trên 2c) Trên tia đối của tia AC lấy điểm E sao cho AE=AC. Chứng minh rằng:BE// AM.d) Tìm điều kiện của tam giác ABC để AC bằng BC trên 2e) Gọi O là trung điểm của AB. Chứng minh rằng: Ba...

Đọc tiếp

#Toán lớp 7

1

S

✰๖ۣۜŠɦαɗøω✰

30 tháng 3 2020

a) Xét tam giác CMA và tam giác BMD có :

\(\hept{\begin{cases}MC=MB\\AM=MD\\\widehat{AMC}=\widehat{BMD}\end{cases}\Rightarrow\Delta CMA=\Delta BMD}\)

=> \(\hept{\begin{cases}AC=BD\\\widehat{BDM}=\widehat{ACM}\end{cases}\Rightarrow BD//AC}\)

=> ACBD là hình bình hành

=> \(\hept{\begin{cases}AB=CD\\AB//CD\end{cases}}\)=> đpcm

b) Xét tam giác ABC và tam giác CDA có :

\(\hept{\begin{cases}AB=CD\\\widehat{CAB}=\widehat{ACD}=90^∗\end{cases}\Rightarrow\Delta ABC=\Delta CDA}\)( Lưu ý : Vì không có dấu kí hiệu " độ " nên em dùng tạm dấu *)

Chung AC

=> AD=BC

=> \(AM=\frac{1}{2}.AD=\frac{1}{2}.BC\)=> đpcm

c) Xét tam giác ABC có :

M là trung điểm BC

A là trung điểm CE

Từ 2 điều trên =>AM là đường trung bình => AM//BE ( đpcm )

e) AM //BE => AD // BE

Tam giác CBE có BA vừa là đường cac ,vừa là trung tuyến => tam giác CBE cân ở B

=> \(\hept{\begin{cases}BC=BE\\AD=BC\end{cases}\Rightarrow AD=EB}\)

Mà AD//BE => ABDE là hình bình hành => AB cắt DE ở trung điểm

=> E,O , D thẳng hàng => đpcm

Đúng(0)

TV

Trần Văn Thái

21 tháng 2 2022

Cho tam giác ABC vuông tại A. Lấy M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD=MA. Chứng minh rằng a) tam giác ABC= tam giác CDA b) AM=½BC

#Toán lớp 7

2

KV

Kiều Vũ Linh

7 tháng 3

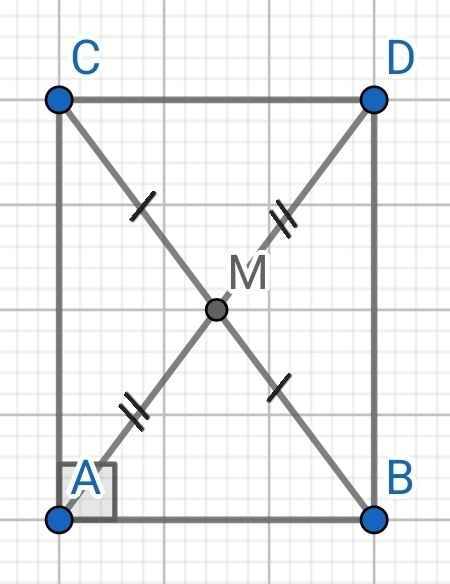
loading...

a) Do M là trung điểm của BC (gt)

⇒ MB = MC

Xét ∆AMB và ∆DMC có:

AM = DM (gt)

∠AMB = ∠DMC (đối đỉnh)

MB = MC (cmt)

⇒ ∆AMB = ∆DMC (c-g-c)

⇒ ∠MAB = ∠MDC (hai góc tương ứng)

Lại có:

∠MAC + ∠MAB = 90⁰ (∆ABC vuông tại A)

⇒ ∠MAC + ∠MDC = 90⁰

⇒ ∠DAC + ∠ADC = 90⁰

∆CDA có:

∠DAC + ∠CDA + ∠ACD = 180⁰ (tổng ba góc trong ∆ACD)

⇒ ∠ACD = 180⁰ - (∠DAC + ∠CDA)

= 180⁰ - 90⁰

= 90⁰

⇒ ∆ACD vuông tại C

Do ∆AMB = ∆DMC (cmt)

⇒ AB = CD (hai cạnh tương ứng)

Xét hai tam giác vuông: ∆ABC và ∆CDA có:

AC là cạnh chung

AB = CD (cmt)

⇒ ∆ABC = ∆CDA (hai cạnh góc vuông)

b) Do ∆ABC = ∆CDA (cmt)

⇒ BC = AD (hai cạnh tương ứng)

Do AM = DM (gt)

⇒ AM = DM = ½AD

Mà AD = BC (cmt)

⇒ AM = ½BC

Đúng(1)

NL

Nguyễn Lê Phước Thịnh

21 tháng 2 2022

a: Xét tứ giác ABDC có

M là trung điểm của AD

M là trung điểm của BC

DO đó: ABDC là hình bình hành

Suy ra: AB=DC; AC=BD

Xét ΔABC và ΔCDA có

AB=CD

BC=DA

AC chung

Do đó: ΔABC=ΔCDA

b: Ta có: ΔABC vuông tại A

mà AM là đường trung tuyến

nên AM=1/2BC

Đúng(2)

TM

Tạ mai anh

26 tháng 2 2020 - olm

Cho tam giác ABC vuông tại A AB lớn hơn AC M là trung điểm của BC trên tia đối của ma lấy điểm D sao cho MD = ma a Chứng minh AB = BC và AB song song bc B Chứng minh tam giác ABC bằng tam giác bda Từ đó suy ra AM = BC chia 2 trên tia đối của AC lấy điểm E sao cho ae = AC Chứng minh Be song song AM đề tìm điều kiện của tam giác ABC để AC = BC chia 2

#Toán lớp 7

1

T

TTYN

26 tháng 2 2020

Hình như đề sai???

Đúng(0)

NA

Ngọc Ánh

19 tháng 4 2021

Co tam giác ABC vuông tại A Lấy đường trung tuyến Am .Trên tia đối của tia MA lấy điểm D sao cho MD=MA a) tính góc ABD b) chứng minh tam giác ABC = tam giacs BAD c) chứng minh AM =1/2 BC

#Toán lớp 7

0

NT

Nguyễn Thị Thu Hiền

16 tháng 4 2019 - olm

Bài 4: Cho tam giác ABC vuông tại A, vẽ trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD=MA

a) Chứng minh : tam giác MAB = tam giác MDC. Suy ra góc ACD vuông

b) Gọi K là trung điểm của AC. Chứng minh: KB=KD

c) KD cắt BC tại I. KB cắt AD tại N. Chứng minh : tam giác KNI cân

#Toán lớp 7

4

DT

Đỗ Thị Dung

17 tháng 4 2019

đề bài sai nhé, bn xem lại câu a

Đúng(0)

NT

Nguyễn Thị Thu Hiền

17 tháng 4 2019

Mình ghi nhầm:

a) Chứng minh: tam giác MAB= tam giác MDC. Suy ra góc ACD vuông

b) Gọi K là trung điểm của AC. Chứng minh: KB=KD

c) KD cắt BC tại I. KB cắt AD tại N. Chứng minh : tam giác KNI cân

Đúng(2)

PT

Phan Tiến Đạt

20 tháng 2 2021

Cho tam giác nhọn ABC, M là trung điểm của BC. Đường vuông góc với AB tại B cắt đường thẳng AM tại D. Trên tia MA lấy điểm E sao cho ME = MD. a,Chứng minh tam giác BMD = tam giác CMEb,chứng minh BD = ECc,Chứng minh EC vuông góc với...

Đọc tiếp

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

20 tháng 2 2021

a) Xét ΔBMD và ΔCME có

BM=CM(M là trung điểm của BC)

\(\widehat{BMD}=\widehat{CME}\)(hai góc đối đỉnh)

MD=ME(gt)

Do đó: ΔBMD=ΔCME(c-g-c)

b) Ta có: ΔBMD=ΔCME(cmt)

nên BD=CE(hai cạnh tương ứng)

c) Ta có: ΔBMD=ΔCME(cmt)

nên \(\widehat{BDM}=\widehat{CEM}\)(hai góc tương ứng)

mà \(\widehat{BDM}\) và \(\widehat{CEM}\) là hai góc ở vị trí so le trong

nên BD//EC(Dấu hiệu nhận biết hai đường thẳng song song)

Ta có: BD//EC(cmt)

BD\(\perp\)AB(gt)

Do đó: EC\(\perp\)AB(Định lí 2 từ vuông góc tới song song)

Đúng(1)

PT

Phan Tiến Đạt

20 tháng 2 2021

cảm ơn nhé bạn

Đúng(0)

RA

ρнươиɢ αин ℓσиєℓу★²κ⁸★ (◡‿◡✿)

19 tháng 4 2021

Cho tam giác ABC cân tại A Kẻ AH vuông góc với BC H thuộc BC Gọi M là trung điểm của BH trên tia đối của tia ma lấy điểm N sao cho MN = MA A) chứng minh rằng tam giác AMH bằng tam giác NMB và NB vuông góc với BC b) Chứng minh rằng AH= MB Từ đó suy ra NB nhỏ hơn AB C) Chứng minh rằng góc BAM nhỏ hơn góc MAH D) Gọi I là trung điểm của NC chứng minh rằng ba điểm A,H,I thẳng hàngPHẢI MẤY THÁNG RỒI MỚI QUAY LẠI ĐÂY ĐÓ...

Đọc tiếp

#Toán lớp 7

0

VT

VO TRAN HOANG LONG

22 tháng 11 2019 - olm

Cho tam giác ABC vuông tại A có góc C=30 độ. Kẻ AK vuông góc với BC ( K thuộc BC). Gọi M là trung điểm của KC. Trên tia đối của tia MA lấy điểm D sao cho MD=MAa/ Chứng minh : Tam giác KMD = tam giác CMAb/ Tính số đo của góc AKDc/ Vẽ KN vuông góc với AB (N thuộc AB) Chứng minh : Ba điểm N, K, D thẳng hàngCho tam giác ABC vuông tại A . Gọi M là trung điểm của cạnh BC. Trên tia đối của tia MA, lấy điểm D sao...

Đọc tiếp

#Toán lớp 7

1

LH

Lê Hồ Trọng Tín

22 tháng 11 2019

Bài 1:

a/Xét \(\Delta KMD\)và \(\Delta CMA\)có:MD=MA(gt);KM=MC(do M là trung điểm KC);^KMD=^CMA(đối đỉnh)

Do đó:\(\Delta KMD=\Delta CMA\left(c.g.c\right)\)

b/\(\Delta KMD=\Delta CMA\left(c.g.c\right)\Rightarrow\widehat{MKD}=\widehat{MCA}\Rightarrow KD//CA\Rightarrow\widehat{CKD}=\widehat{ACB}=30^0\Rightarrow\widehat{AKD}=90^0+30^0=120^0\)c/Ta có KN//AC(do cùng vuông góc với AB),mà KD//CA nên K;N;D thẳng hàng

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP