Cho phương trình: 2x3+3x2-mx+m-5=0
Tìm m để phương trình có:
a)Đúng 1 nghiệm
b)3 nghiệm phân biệt >0
c)3 nghiệm phân biệt thoả mãn:x13+x22+x32≤20
d) 3 nghiệm phân biệt <2.
Giúp nhanh cho tớ bây giờ với ạ.Cảm ơn rất nhiều ạ!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Xét y = 2x3 – 3x2 + 1
Ta có: y’ = 6x2 – 6x
ð y’ = 0 ⇔ x = 0 hoặc x = 1
Ta có bảng biến thiên
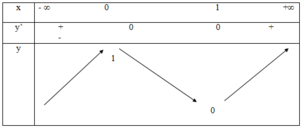
Số nghiệm phương trình đã cho m = 2x3 – 3x2 + 1
= Số giao điểm của đồ thị hàm số y = 2x3 – 3x2 + 1 và đường thẳng y = m
-> 0<m<1

\(x^3-5x^2+2mx+5x-4m+2=0\)
\(\Leftrightarrow\left(x^3-5x^2+5x+2\right)+2m\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2-3x-1\right)+2m\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2-3x+2m-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x^2-3x+2m-1=0\left(1\right)\end{matrix}\right.\)
a. Pt đã cho có 3 nghiệm pb khi và chỉ khi (1) có 2 nghiệm pb khác 2
\(\Leftrightarrow\left\{{}\begin{matrix}4-6+2m-1\ne0\\\Delta=9-4\left(2m-1\right)>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{3}{2}\\m< \dfrac{13}{8}\end{matrix}\right.\)
b. Do vai trò 3 nghiệm như nhau, không mất tính tổng quát, giả sử \(x_1;x_2\) là nghiệm của (1) và \(x_3=2\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=2m-1\end{matrix}\right.\)
\(x_1^2+x_2^2+x_3^2=11\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+4=11\)
\(\Leftrightarrow9-2\left(2m-1\right)-7=0\)
\(\Leftrightarrow m=1\)

∆ = m² - 4(m - 5)
= m² - 4m + 5
= (m² - 4m + 4) + 1
= (m - 2)² + 1 > 0 với mọi m
Phương trình luôn có 2 nghiệm phân biệt
Theo Viét ta có:
x₁ + x₂ = m (1)
x₁.x₂ = m - 5 (2)
x₁ + 2x₂ = 1 (3)
Lấy (3) - (1) ta được x₂ = 1 - m thay vào (1) ta được
x₁ + 1 - m = m
⇔ x₁ = 2m - 1
Thay x₁ = 2m - 1 và x₂ = 1 - m vào (2) ta được:
(2m - 1)(1 - m) = m - 5
⇔ 2m - 2m² - 1 + m - m + 5 = 0
⇔ -2m² + 2m + 5 = 0
∆ = 4 - 4.(-2).5
= 44
m₁ = -1 + √11
m₂ = -1 - √11
Vậy m = -1 + √11; m = -1 - √11 thì phương trình đã cho có hai nghiệm thỏa mãn x₁ + 2x₂ = 1

a) Ta có: \(\Delta=\left(-4\right)^2-4\cdot1\cdot\left(2m-3\right)=16-4\left(2m-3\right)\)
\(\Leftrightarrow\Delta=16-8m+12=-8m+28\)
Để phương trình có hai nghiệm x1;x2 phân biệt thì \(-8m+28>0\)
\(\Leftrightarrow-8m>-28\)
hay \(m< \dfrac{7}{2}\)
Với \(m< \dfrac{7}{2}\) thì phương trình có hai nghiệm phân biệt x1;x2
nên Áp dụng hệ thức Viet, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-\left(-4\right)}{1}=4\\x_1\cdot x_2=\dfrac{2m-3}{1}=2m-3\end{matrix}\right.\)
Để phương trình có hai nghiệm x1,x2 phân biệt thỏa mãn tổng 2 nghiệm và tích hai nghiệm là hai số đối nhau thì
\(\left\{{}\begin{matrix}m< \dfrac{7}{2}\\4+2m-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{7}{2}\\2m+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{7}{2}\\2m=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{7}{2}\\m=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m=-\dfrac{1}{2}\)
Vậy: Khi \(m=-\dfrac{1}{2}\) thì phương trình có hai nghiệm x1,x2 phân biệt thỏa mãn tổng 2 nghiệm và tích hai nghiệm là hai số đối nhau

\(\text{Δ}=\left(2m+2\right)^2-4\left(m+3\right)\)
\(=4m^2+8m+4-4m-12\)
\(=4m^2+4m-8\)
\(=4\left(m+2\right)\left(m-1\right)\)
Để phương trình có hai nghiệm phân biệt thì (m+2)(m-1)>0
=>m>1 hoặc m<-2
Theo đề, ta có: 2(m+1)>2
=>m+1>1
hay m>0
=>m>1

a) \(\Delta=\left[-\left(m+3\right)\right]^2-4.1.m\\ =m^2+6m+9-4m\\ =m^2+2m+9\\ =\left(m+1\right)^2+8>0\forall m\)
Vậy phương trình luôn có 2 nghiệm phân biệt với mọi m.
b) Áp dụng hệ thức Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=m+3\\x_1x_2=m\end{matrix}\right.\)
Mà \(x_1^2+x_2^2=6\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=6\\ \Leftrightarrow\left(m+3\right)^2-2m=6\\ \Leftrightarrow m^2+6m+9-2m=6\\ \Leftrightarrow m^2+4m+3=0\\ \Leftrightarrow\left(m+1\right)\left(m+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-1\\m=-3\end{matrix}\right.\)
Vậy \(m\in\left\{-1;-3\right\}\) là các giá trị cần tìm.
a, Ta có: \(\Delta=\left[-\left(m+3\right)\right]^2-4.1.m\)
\(=m^2+6m+9-4m\)
\(=m^2+2m+9\)
\(=m^2+2m+1+8\)
\(=\left(m+1\right)^2+8\)
Lại có: \(\left(m+1\right)^2\ge0\forall m\Rightarrow\left(m+1\right)^2+8\ge8\forall m\)
Vậy phương trình luôn có 2 nghiêm phân biệt
b, Theo hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=m+3\\x_1+x_2=m\end{matrix}\right.\)
Theo bài ra:
\(x_1^2+x_2^2=6\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=6\)
\(\Leftrightarrow\left(m+3\right)^2-2m=6\)
\(\Leftrightarrow m^2+6m+9-2m=6\)
\(\Leftrightarrow m^2+6m+9-2m-6=0\)
\(\Leftrightarrow m^2+4m+3=0\)
\(\Leftrightarrow m^2+m+3m+3=0\)
\(\Leftrightarrow\left(m^2+m\right)+\left(3m+3\right)=0\)
\(\Leftrightarrow m\left(m+1\right)+3\left(m+1\right)=0\)
\(\Leftrightarrow\left(m+1\right)\left(m+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m+1=0\\m+3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-1\\m=-3\end{matrix}\right.\)
Vậy với m=-1 hoặc m=-3 thì phương trinh trên thỏa mãn hệ thức