Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
· Điều kiện cần:
Giả sử phương trình đã cho có 3 nghiệm phân biệt x 1 ; x 2 ; x 3 lập thành một cấp số cộng
Khi đó: x 1 + x 3 = 2 x 2 x 1 + x 2 + x 3 = 3 ⇔ 3 x 2 = 3 ⇔ x 2 = 1 .
Với x 2 = 1 thay vào phương trình ta được:
1 − 3 + m + 2 − m = 0 (luôn đúng).
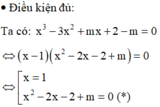
Phương trình đã cho có 3 nghiệm phân biệt tương đương với phương trình (*) có 2 nghiệm phân biệt khác 1.
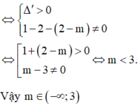

Đáp án B
Phương pháp: Đặt t = 2 x
Cách giải: Đặt t = 2 x ta có:
![]()
Khi đó phương trình trở thành
![]()
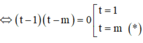
![]()
![]()
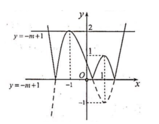
Để phương trình ban đầu có 3 nghiệm phân biệt ![]() có nghiệm
có nghiệm ![]()

Đáp án C
Xét hàm số f x = x 3 − 3 x 2 + 1 có:
f ' x = 3 x 2 − 6 x = 3 x x − 2 ⇒ f ' x = 0 ⇔ x = 0 x = 2
Ta có bảng biến thiên của như sau:
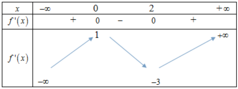
Từ bảng biến thiên này ta có bang biến thiên của f x = x 3 − 3 x + 1 như sau:
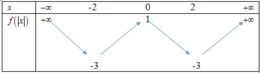
Dựa trên bảng biến thiên này ta thấy PT:
x 3 − 3 x 2 + 1 - m = 0 ⇔ x 3 − 3 x 2 + 1 = m có 4 nghiệm phân biệt ⇔ − 3 < m < 1

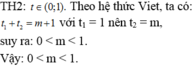





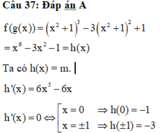

Đáp án C
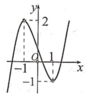
Xét y = 2x3 – 3x2 + 1
Ta có: y’ = 6x2 – 6x
ð y’ = 0 ⇔ x = 0 hoặc x = 1
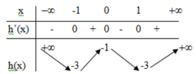
Ta có bảng biến thiên
Số nghiệm phương trình đã cho m = 2x3 – 3x2 + 1
= Số giao điểm của đồ thị hàm số y = 2x3 – 3x2 + 1 và đường thẳng y = m
-> 0<m<1