Hai đường thẳng xx' và yy' cắt nhau tại O tạo thành 4 góc, trong đó tổng 2 góc xOy và x'Oy = 248 độ. Số đo góc xOy' là ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 6 2018
Sai đề rồi bạn nha . Mk chứng minh lỗi nha
Vì đường thằng \(xx'\)cắt \(yy'\)tại \(O\)
\(\Rightarrow xOx'=180^o\)
Vì \(xx'\)là 1 đường thẳng .
[ \(Ox\)đối với \(Ox'\)]
Vì vậy nên \(xOy+yOx'=180^o\)( cắt tại O )
PA
22 tháng 5 2016
Mik xin lỗi, mik đọc sai đề
Mik giải lại nhé
\(xOy+x'Oy'=248^0\)
mà \(xOy=x'Oy'\) (2 góc đối đỉnh)
\(\Rightarrow xOy=x'Oy'=\frac{248^0}{2}=124^0\)
\(xOy+xOy'=180^0\) (2 góc kề bù)
\(124^0+xOy'=180^0\)
\(xOy'=180^0-124^0\)
\(xOy'=56^0\)
Chúc bạn học tốt
KN
15 tháng 7 2023
\(\widehat{xOy}+\widehat{x'Oy=180^0}\) (Vì \(\widehat{xOy}\) và \(\widehat{x'Oy}\) là hai góc kề bù)
\(\widehat{xOy}-\widehat{x'Oy}=40^0\)
a.\(\widehat{xOy}=\left(180^0+40^0\right):2=110^0\)
\(\widehat{x'Oy'}=\widehat{xOy}=110^0\) ( 2 góc đối đỉnh)
b. \(\widehat{x'Oy}=180^0-\widehat{xOy}=180^0-110^0=70^0\) (2 góc kề bù)
\(\widehat{xOy'}=\widehat{x'Oy}=70^0\) ( 2 góc đối đỉnh)
BY
0
C
19 tháng 1 2023
Ta có :
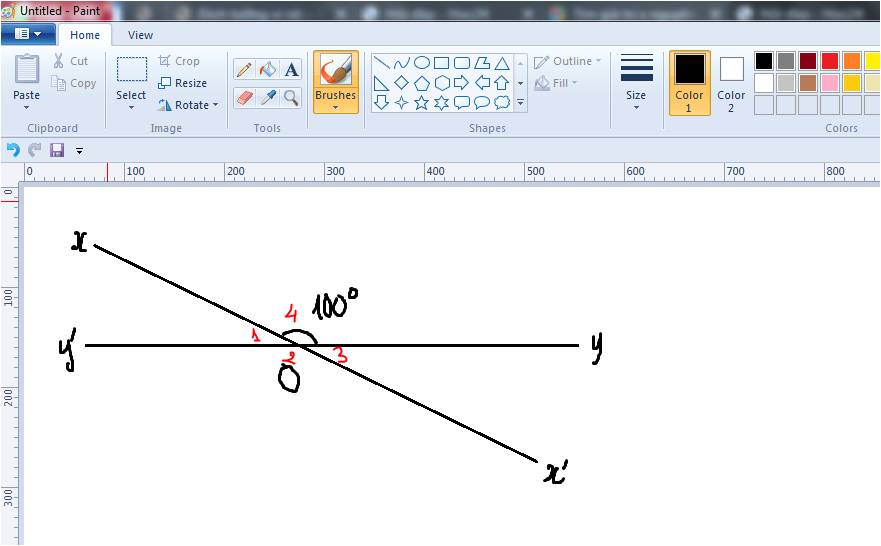
`@)` `\hat{x'Oy'} = \hat{xOy} = 100^@` (hai góc đối đỉnh)
`@)` `\hat{xOy + \hat{xOy'} = 180^@`
hay `100 +` `\hat{xOy'} = 180^@`
`⇒\hat{xOy'} = 180^@ - 100^@ = 80^@`
`@)` `\hat{x'Oy} = \hat{xOy'} = 80^@` (hai góc đối đỉnh)
Đề sai rồi bạn