một vật đi một phần đường trong thời gian t1 với tốc độ t1 , đi phần còn lại trong t2 với vận tốc v2 a) tìm vtb của vật trên cả quãng đường b) trong điều kiện nào thì vận tốc trung bình bằng tổng trung bình cộng của v1 vag v2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C
Công thức tính vận tốc trung bình của người này trên hai quãng đường s1 và s2 là:
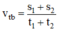

Rải
Ta có:
\(V_{tb}=\dfrac{S_{AB}+S_{BC}}{t_1+t_2}=\dfrac{v_1.t_1+v_2.t_2}{t_1+t_2}\left(1\right)\)
\(V_{tb}=\dfrac{v_1+v_2}{2}\left(2\right)\)
Từ (1) và (2)<=>\(\dfrac{v_1+v_2}{2}=\dfrac{v_1t_1+v_2t_2}{t_1+t_2}\)
<=>\(\left(v_1+v_2\right)\left(t_1+t_2\right)=2v_1.t_1+2v_2.t_2\)
<=>\(v_1.t_1+v_1.t_2+v_2.t_1+v_2.t_2=2v_1.t_1+2v_2.t_2\)
<=>\(v_1.t_2+v_2.t_1=v_1.t_1+v_2.t_2\)
<=>\(t_2\left(v_1-v_2\right)=t_1\left(v_1-v_2\right)\)
<=>\(t_2=t_1.\)
Vậy \(t_1=t_2\).

a) Thời gian vật đi hết quãng đường trên:
\(t_{tổng}=t_1+t_2=\dfrac{S_1}{v_1}+\dfrac{S_2}{v_2}=\dfrac{520:2}{5}+\dfrac{520:2}{7}=\dfrac{624}{7}\left(s\right)\)
b) Thời gian vật đi quãng đường T1 và quãng đường T2:
\(\left\{{}\begin{matrix}t_1=\dfrac{S_1}{v_1}=\dfrac{520:2}{5}=52\left(s\right)\\t_2=\dfrac{S_2}{v_2}=\dfrac{520:2}{7}=\dfrac{260}{7}\left(\dfrac{m}{s}\right)\end{matrix}\right.\)
Vận tốc trung bình trên cả quãng đường:
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{520}{52+\dfrac{260}{7}}=\dfrac{35}{6}\left(\dfrac{m}{s}\right)\)

Vận tốc trung bình của xe là:
\(v_{tb}=\dfrac{30+30}{10+30}=1,5\left(\dfrac{m}{s}\right)\)
Chọn D
Vận tốc trung bình của vật trên đoạn đường AB là
\(vtb\)= \(\dfrac{30+30}{10+30}\)=1,5 (m/s)
D nha

Đáp án B
Vật tốc trung bình của người đi xe đạp đó là: v = s 1 + s 2 + s 3 t 1 + t 2 + t 3


DươngDương câu b tương tự bài hum đó này trng trường hợp nào thì
Nguyễn Hải Dương bài này khác, cái đề cho tốc độ t1 mà :)