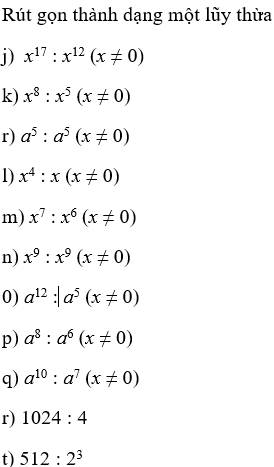Giải chi tiết giúp mik vs
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 67:
Đổi 5,1 tấn = 5100 kg
Ta có: \(n_{NH_3}=\dfrac{5100}{17}=300\left(kmol\right)\)
Bảo toàn Nitơ: \(n_{NH_3}=n_{HNO_3\left(lý.thuyết\right)}=300\left(kmol\right)\)
\(\Rightarrow m_{ddHNO_3\left(thực\right)}=\dfrac{300\cdot40\%\cdot63}{63\%}=12000\left(kg\right)=12\left(tấn\right)\)
Câu 68:
Ta có: \(n_{HNO_3\left(thực\right)}=\dfrac{400\cdot12,6\%}{63}=0,8\left(mol\right)\) \(\Rightarrow n_{HNO_3\left(lý.thuyết\right)}=\dfrac{0,8}{40\%}=2\left(mol\right)\)
Bảo toàn Nitơ: \(n_{NH_3}=n_{HNO_3\left(lý.thuyết\right)}=2\left(mol\right)\) \(\Rightarrow V_{NH_3}=2\cdot22,4=44,8\left(l\right)\)

1) \(=\left(2x\right)^2-3^2=\left(2x-3\right)\left(2x+3\right)\)
2) \(=8^2-\left(5y\right)^2=\left(8-5y\right)\left(8+5y\right)\)
3) \(=1-\left(7x\right)^2=\left(1-7x\right)\left(1+7x\right)\)
4) \(=\left(16xy\right)^2-1=\left(16xy-1\right)\left(16xy+1\right)\)
5) \(=2\left(x^2-9y^2\right)=2\left(x-3y\right)\left(x+3y\right)\)
6) \(=3\left(a^2-4b^4\right)=3\left(a-2b^2\right)\left(a+2b^2\right)\)
7) \(=\left(a^2\right)^2-4^2=\left(a^2-4\right)\left(a^2+4\right)=\left(a-2\right)\left(a+2\right)\left(a^2+4\right)\)
8) \(=9^2-\left(x^2\right)^2=\left(9-x^2\right)\left(9+x^2\right)=\left(3-x\right)\left(3+x\right)\left(9+x^2\right)\)
9) \(=\left(6b\right)^2-a^2=\left(6b-a\right)\left(6b+a\right)\)
10) \(=\left(8x^3\right)^2-27^2=\left(8x^3-27\right)\left(8x^3+27\right)=\left(2x-3\right)\left(4x^2+6x+9\right)\left(2x+3\right)\left(4x^2-6x+9\right)\)

`@` `\text {Ans}`
`\downarrow`
`j)`
\(x^{17}\div x^{12}=x^{17-12}=x^5\)
`k)`
\(x^8\div x^5=x^{8-5}=x^3\)
`r)`
\(a^5\div a^5=a^{5-5}=a^0=1\)
`l)`
\(x^4\div x=x^{4-1}=x^3\)
`m)`
\(x^7\div x^6=x^{7-6}=x\)
`n)`
\(x^9\div x^9=x^{9-9}=x^0=1\)
`o)`
\(a^{12}\div a^5=a^{12-5}=a^7\)
`p)`
\(a^8\div a^6=a^{8-6}=a^2\)
`q)`
\(a^{10}\div a^7=a^{10-7}=a^3\)
`r(2),`
\(1024\div4=2^{10}\div2^2=2^8\)
`t)`
\(512\div2^3=2^9\div2^3=2^6\)

1:
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
mà góc BAC=90 độ
nên ABDC là hình chữ nhật
=>AB//CD và AB=CD
b: Xét ΔABC và ΔCDA có
AB=CD
BC=DA
AC chung
=>ΔABC=ΔCDA
c: ΔCBA vuông tại A
mà AM là trung tuyến
nên AM=BC/2

a: Xét tứ giác MNQP có
I là trung điểm của NP
I là trung điểm của MQ
Do đó: MNQP là hình bình hành
mà MQ=NP
nên MNQP là hình chữ nhật

\(A=-\left(x^2-4x+4\right)-\left(y^2+4y+4\right)+10\\ A=-\left(x-2\right)^2-\left(y+2\right)^2+10\le10\\ A_{max}=10\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-2\end{matrix}\right.\)