tìm 3 số nguyên liên tiếp biết tổng các bình phương số đầu bằng bình phương số cuối
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 9 2016
Gọi 3 số đó là a - 1 ; a ; 1 + a
Ta có :
\(a^2+\left(a-1\right)^2=\left(a+1\right)^2\)
\(a^2+a^2+1-2a=a^2+1+2a\)
\(a^2-2a=2a\)
\(a^2=4a\)
\(a^2-4a=0\)
\(a\left(a-4\right)=0\)
\(\Rightarrow\orbr{\begin{cases}a=0\\a=4\end{cases}}\)
Vậy...
HP
1 tháng 10 2016
Gọi 3 số tự nhiên liên tiếp lần lượt là a,a+1,a+2 (a \(\in\) N)
Có: a2+(a+1)2=(a+2)2
=>a2+a2+2a+1=a2+4a+4
=>a2+2a+1=4a+4
=>a2+1=2a+4
=>a2+1-2a-4=0
=>a2-2a-3=0
=>a2-3a+a-3=0
=>a(a-3)+(a-3)=0
=>(a+1)(a-3)=0
=>a=-1 hoặc a=3
Mà a \(\in\) N
=>a=3
Vậy STN nhỏ nhất là 3
1 tháng 10 2016
Gọi 3 số đó là a ; a + 1 và a + 2
Có :
\(a^2+\left(a+1\right)^2=\left(a+2\right)^2\)
\(2a^2+2a+1=a^2+4+4a\)
\(\Rightarrow a^2=3+2a\)
\(a^2-2a-3=0\)
\(\left(a^2-3a\right)+\left(a-3\right)=0\)
\(\left(a-3\right)\left(a+1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}a=3\\a=-1\end{cases}}\)
Mà a là số tự nhiên nên a = 3
Vậy ...
MQ
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
25 tháng 1 2019
Gọi 7 số nguyên liên tiếp là: n; n+1; n+2; n+3; n+4; n+5; n+6. Theo đề bài
\(n^2+\left(n+1\right)^2+\left(n+2\right)^2+\left(n+3\right)^2=\left(n+4\right)^2+\left(n+5\right)^2+\left(n+6\right)^2.\)
Khai triển, rút gọn rồi giải phương trình bậc 2 để tìm n phù hợp
CM
23 tháng 12 2018
Đáp án C
Gọi d = 2 x là công sai
ta có bốn số là a - 3 x , a - x , a + x , a + 3 x
Khi đó, từ giả thiết ta có:
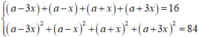
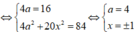
⇔ 1 , 3 , 5 , 7 7 , 5 , 3 , 1
Tổng bình phương của số hạng đầu và cuối là 1 2 + 7 2 = 50
CM
13 tháng 1 2019
Đáp án C.
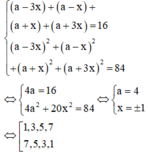
Tổng bình phương của số hạng đầu và cuối là 1 2 + 7 2 = 50
PT
1
Gọi 3 số nguyên liên tiếp là a-1, a, a+1 (a ∈ Z)
Theo đề ta có \(\left(a-1\right)^2+a^2=\left(a+1\right)^2\)
\(\Leftrightarrow a^2-2a+1+a^2=a^2+2a+1\)
\(\Leftrightarrow a^2-4a=0\)
\(\Leftrightarrow a\left(a-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=0\\a=4\end{matrix}\right.\)
Vậy có 2 cặp 3 số nguyên liên tiếp đó là \(\left(-1;0;1\right)\) và \(\left(3;4;5\right)\)
Tick nha bạn 😘