Chứng minh rằng:
(X-2)(X+3)=X2+x-6
Cam ơn nka
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
3 tháng 10 2023
Bài 4.
\(A=2x^3+(x+1)^3-3x(x-2)(x+2)-3(x^2+5x+9)\\=2x^3+(x^3+3x^2+3x+1)-3x(x^2-4)-3x^2-15x-27\\=2x^3+x^3+3x^2+3x+1-3x^3+12x-3x^2-15x-27\\=(2x^3+x^3-3x^3)+(3x^2-3x^2)+(3x+12x-15x)+(1-27)\\=-26\\---\)
\(B=x(x-4x)+x(2-x)(x+2)+4(2x^2-5x+4)\\=x\cdot(-3x)+x(2-x)(2+x)+8x^2-20x+16\\=-3x^2+x(4-x^2)+8x^2-20x+16\\=-3x^2+4x-x^3+8x^2-20x+16\)
Bạn kiểm tra lại đề giúp mình!
\(C=(x-2y)(x^2+2xy+4y^2)-(x^3-8y^3+10)\) (sửa đề)
\(=x^3-(2y)^3-x^3+8y^2-10\\=x^3-8y^3-x^3+8y^3-10\\=(x^3-x^3)+(-8y^3+8y^3)-10\\=-10\)
Bài 5.
\(d)xy^2-3x^3y^2-2x(xy-3xy^2)\\=xy^2-3x^3y^2-2x^2y+6x^2y^2\\---\\f)(x-y)(2x+y)-2x^2+y^2+3xy\\=x(2x+y)-y(2x+y)-2x^2+y^2+3xy\\=2x^2+xy-2xy-y^2-2x^2+y^2+3xy\\=(2x^2-2x^2)+(xy-2xy+3xy)+(-y^2+y^2)\\=2xy\)
\(Toru\)
AH
Akai Haruma
Giáo viên
22 tháng 7 2021
Lời giải:
a.
$A=(x+6)^2-(x+2)^2+2[(x-5)^2-(x-3)^2]$
$=(x+6-x-2)(x+6+x+2)+2[(x-5-x+3)(x-5+x-3)]$
$=4(2x+8)+2(-2)(2x-8)$
$=4(2x+8)-4(2x-8)=4[(2x+8)-(2x-8)]=4.16=64$ không phụ thuộc vào $x$
b.
$B=(x^3-2^3)-(x^3+2^3)=-16$ không phụ thuộc vào $x$
c.
$C=x^4+2x^2-[(x^2+3)^2-(2x)^2]$
$=x^4+2x^2-(x^4+6x^2-4x^2)$
$=x^4+2x^2-(x^4+2x^2)=0$ không phụ thuộc vào $x$
22 tháng 7 2021
a) Ta có: \(A=\left(x+6\right)^2+2\left(x-5\right)^2-\left(x+2\right)^2-2\left(x-3\right)^2\)
\(=x^2+12x+36+2\left(x^2-10x+25\right)-\left(x^2+4x+4\right)-2\left(x^2-6x+9\right)\)
\(=x^2+12x+36+2x^2-20x+50-x^2-4x-4-2x^2+12x-18\)
\(=34\)
b) Ta có: \(B=\left(x-2\right)\left(x^2+2x+4\right)-\left(x+2\right)\left(x^2-2x+4\right)\)
\(=x^3-8-x^3-8\)
=-16
c) Ta có: \(C=x^4+2x^2-\left(x^2-2x+3\right)\left(x^2+2x+3\right)\)
\(=x^4+2x^2-\left[\left(x^2+3\right)^2-4x^2\right]\)
\(=x^4+2x^2-\left(x^4+6x^2+9\right)+4x^2\)
\(=-9\)
17 tháng 7 2021
a) Ta có: \(\dfrac{x^2+2x+1}{x^2+x}\)
\(=\dfrac{\left(x+1\right)^2}{x\left(x+1\right)}\)
\(=\dfrac{x+1}{x}\)
b) Ta có: \(\dfrac{x^2-4x+3}{x^2-x}\)
\(=\dfrac{\left(x-1\right)\left(x-3\right)}{x\left(x-1\right)}\)
\(=\dfrac{x-3}{x}\)
CM
31 tháng 7 2018
Thực hiện khai triển hằng đẳng thức
A = ( x 3 – 1) + ( x 3 – 6 x 2 + 12x – 8) – 2( x 3 + 1) + 6( x 2 – 2x + 1).
Rút gọn A = -5 không phụ thuộc biến x.
PT
0
CM
23 tháng 1 2017
Biểu thức x x - 3 - x 2 + 3 x 2 x + 3 . x + 3 x 2 - 3 x - x x 2 - 9 xác định khi x – 3 ≠ 0,2x + 3 ≠ 0, x 2 - 3 x ≠ 0 và x 2 - 9 ≠ 0
Suy ra: x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ 3 và x ≠ ± 3
Với điều kiện x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ - 3, ta có:
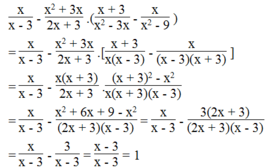
Vậy giá trị của biểu thức x x - 3 - x 2 + 3 x 2 x + 3 . x + 3 x 2 - 3 x - x x 2 - 9 bằng 1 khi x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ - 3
10 tháng 9 2023
a) \(x^2+xy+y^2+1\)
\(=x^2+xy+\dfrac{y^2}{4}-\dfrac{y^2}{4}+y^2+1\)
\(=\left(x+\dfrac{y}{2}\right)^2+\dfrac{3y^2}{4}+1\)
mà \(\left\{{}\begin{matrix}\left(x+\dfrac{y}{2}\right)^2\ge0,\forall x;y\\\dfrac{3y^2}{4}\ge0,\forall x;y\end{matrix}\right.\)
\(\Rightarrow\left(x+\dfrac{y}{2}\right)^2+\dfrac{3y^2}{4}+1>0,\forall x;y\)
\(\Rightarrow dpcm\)
10 tháng 9 2023
b) \(...=x^2-2x+1+4\left(y^2+2y+1\right)+z^2-6z+9+1\)
\(=\left(x-1\right)^2+4\left(y^{ }+1\right)^2+\left(z-3\right)^2+1>0,\forall x.y\)
\(\Rightarrow dpcm\)
MM
0
vế phải, vế trái
\(VP=x^2+x-6=x^2+2x-3x-6=x\left(x+2\right)-3\left(x+2\right)=\left(x-3\right)\left(x+2\right)=VT\left(\text{đ}pcm\right)\)