Số cặp số nguyên dương để biểu thức
nhận giá trị là số nguyên
là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
VD
2
Những câu hỏi liên quan
13 tháng 9 2016
Ta có
\(\frac{3x+3y+5}{x+y}=3+\frac{5}{x+y}\)
Để P nguyên thì x + y phải là ước của 5 hay
(x + y) = (1; 5)
Thế vào rồi giải ra
18 tháng 9 2016
\(P=\frac{3x+3y+5}{x+y}=\frac{3\left(x+y\right)+5}{x+y}=3+\frac{5}{x+y}\)mà\(P\in Z\Rightarrow\frac{5}{x+y}\in Z\)mà\(x,y\ge1\Rightarrow x+y\ge2\)
=> x + y = 5 (vì 5 là ước nguyên của 5).Có 4 cặp (x ; y) thỏa mãn đề là (1 ; 4);(2 ; 3);(3 ; 2);(4 ; 1)
4 tháng 12 2017
Vì các số 3 ; x ; y ; 6 ; 1 đều là các số nguyên
Nên x; y thuộc mọi giá trị nguyên thì H vẫn là số nguyên
12 tháng 7 2023
Để A là số nguyên thì n-4 chia hết cho 4n-8
=>4n-16 chia hết cho 4n-8
=>4n-8-8 chia hết cho 4n-8
=>4n-8 thuộc Ư(-8)
=>4n-8 thuộc {1;-1;2;-2;4;-4;8;-8}
mà n là số nguyên dương
nên n thuộc {3;1;4}
30 tháng 5 2016
a) Để \(\frac{11}{\sqrt{x}-5}\)nhận giá trị nguyên thì \(\sqrt{\text{x}}-5\inƯ\left(11\right)\)(DK : \(0\le x\ne25\))
Vì \(\sqrt{\text{x}}-5\ge-5\)nên ta có :
\(\sqrt{x}-5\in\left\{-1;1;11\right\}\)\(\Rightarrow\sqrt{x}\in\left\{4;6;16\right\}\Rightarrow x\in\left\{16;36;256\right\}\)
b) \(B=\frac{\sqrt{x}+1}{\sqrt{x}-3}=\frac{\sqrt{x}-3+4}{\sqrt{x}-3}=1+\frac{4}{\sqrt{x}-3}\)(DK : \(0\le x\ne9\))
Để B nhận giá trị nguyên thì \(\sqrt{x}-3\inƯ\left(4\right)\)
Vì \(\sqrt{\text{x}}-3\ge-3\)nên ta có :
\(\sqrt{\text{x}}-3\in\left\{-2;-1;1;2;4\right\}\)\(\Rightarrow\sqrt{x}\in\left\{1;2;4;5;7\right\}\Rightarrow x\in\left\{1;4;16;25;49\right\}\)
21 tháng 12 2021
a) ĐK:\(\begin{cases} x + 2≠0\\ x - 2≠0 \end{cases}\)⇔\(\begin{cases} x ≠ -2\\ x≠ 2 \end{cases}\)
Vậy biểu thức P xác định khi x≠ -2 và x≠ 2
b) P= \(\dfrac{3}{x+2}\)-\(\dfrac{2}{2-x}\)-\(\dfrac{8}{x^2-4}\)
P=\(\dfrac{3}{x+2}\)+\(\dfrac{2}{x-2}\)-\(\dfrac{8}{(x-2)(x+2)}\)
P= \(\dfrac{3(x-2)}{(x-2)(x+2)}\)+\(\dfrac{2(x+2)}{(x-2)(x+2)}\)-\(\dfrac{8}{(x-2)(x+2)}\)
P= \(\dfrac{3x-6+2x+4-8}{(x-2)(x+2)}\)
P=\(\dfrac{5x-10}{(x-2)(x+2)}\)
P=\(\dfrac{5(x-2)}{(x-2)(x+2)}\)
P=\(\dfrac{5}{x+2}\)
Vậy P=\(\dfrac{5}{x+2}\)
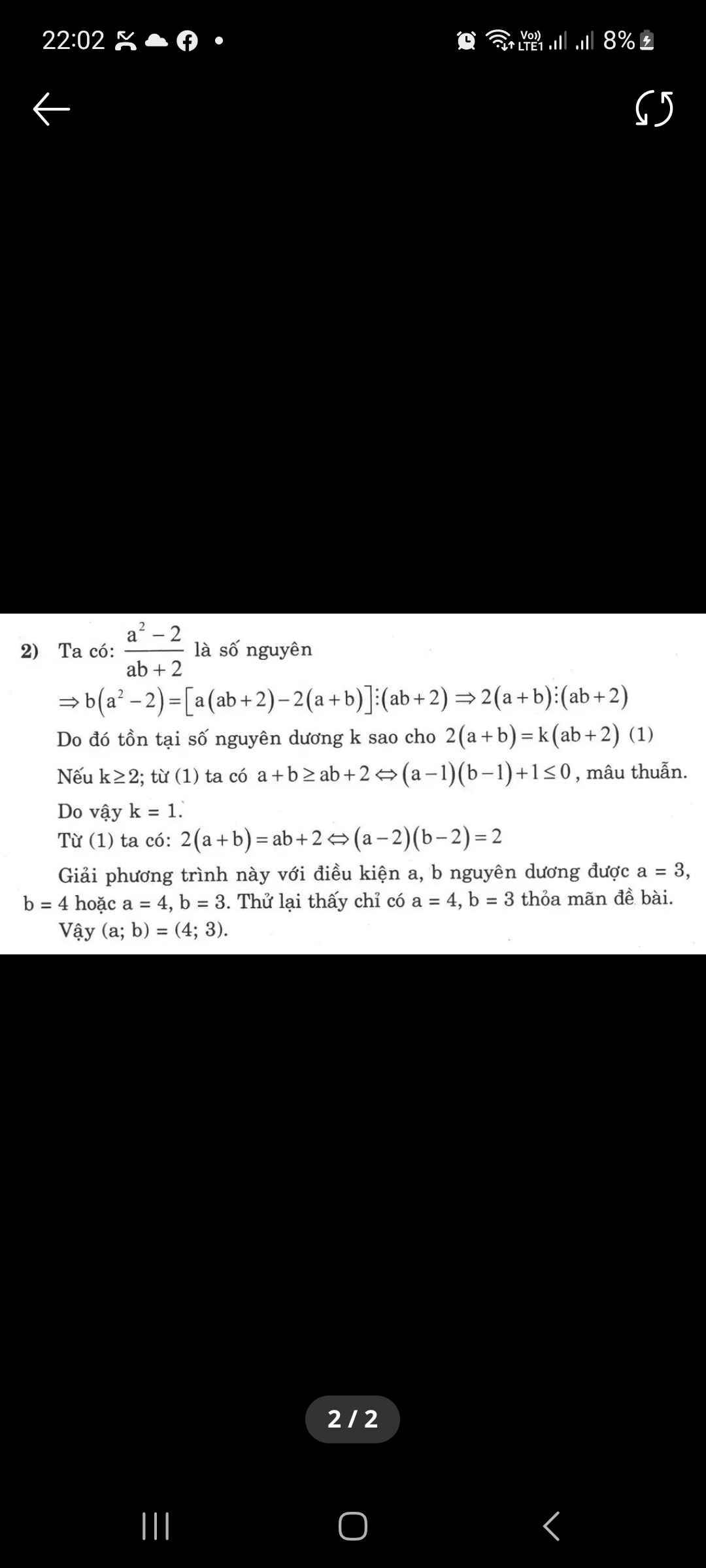
Ta có :
\(P=3+\frac{5}{x+y}\)
\(P\in Z\Leftrightarrow\frac{5}{x+y}\in Z\Leftrightarrow x+y\inƯ_5\)
\(\Rightarrow\left(x;y\right)\in\left\{\left(1;4\right);\left(2;3\right);\left(4;1\right);\left(3;2\right)\right\}\)
\(P=\frac{3x+3y+5}{x+y}=\frac{3\left(x+y\right)}{x+y}+\frac{5}{x+y}=3+\frac{5}{x+y}\)
P thuộc Z
<=> x + y thuộc Ư(5)
<=> x = 1 và y = 4 ; x = 2 và y = 3 ; x = 3 và y = 2 ; x = 4 và y = 1