Cho các số thực x,y thoả mãn : x4 +y4 +x2 -3 = 2y2 (1-x2) tìm giá trị lớn nhất,giá trị nhỏ nhất của B= x2 +y2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^2+y^2=1+xy\Rightarrow x^2+y^2-xy=1\)
Ta có: \(1+xy=x^2+y^2\ge2xy\Rightarrow xy\le1\)
\(1+xy=x^2+y^2\ge-2xy\Rightarrow xy\ge-\dfrac{1}{3}\)
\(P=\left(x^2+y^2\right)^2-x^2y^2-2x^2y^2=\left(x^2+y^2-xy\right)\left(x^2+y^2+xy\right)-2x^2y^2\)
\(=x^2+y^2+xy-2x^2y^2=-2x^2y^2+2xy+1\)
Đặt \(a=xy\Rightarrow P=f\left(a\right)=-2a^2+2a+1\)
Xét hàm \(f\left(a\right)=-2a^2+2a+1\) trên \(\left[-\dfrac{1}{3};1\right]\)
\(-\dfrac{b}{2a}=\dfrac{1}{2}\in\left[-\dfrac{1}{3};1\right]\)
\(f\left(-\dfrac{1}{3}\right)=\dfrac{1}{9}\) ; \(f\left(\dfrac{1}{2}\right)=\dfrac{3}{2}\) ; \(f\left(1\right)=1\)
\(\Rightarrow M=\dfrac{3}{2}\) ; \(m=\dfrac{1}{9}\) \(\Rightarrow Mm=\dfrac{1}{6}\)

Lời giải:
$A=(x+y)(x^2-xy+y^2)+x^2+y^2=2(x^2-xy+y^2)+x^2+y^2=2(x^2+y^2)+(x-y)^2$
$\geq 2(x^2+y^2)=(1^2+1^2)(x^2+y^2)\geq (x+y)^2=2^2=4$ (theo BĐT Bunhiacopxky)
Vậy $A_{\min}=4$. Giá trị này đạt tại $x=y=1$

\(P-\dfrac{5}{2}=x+2y-\dfrac{x^2+y^2}{2}=-\dfrac{1}{2}\left(x-1\right)^2-\dfrac{1}{2}\left(y-2\right)^2+\dfrac{5}{2}\le\dfrac{5}{2}\)
\(\Rightarrow P-\dfrac{5}{2}\le\dfrac{5}{2}\Rightarrow P\le5\)
\(P_{max}=5\) khi \(\left(x;y\right)=\left(1;2\right)\)

Áp dụng BĐT cói cho 2 số ko âm ta có
X^2+y^2 >= 2 .căn x^2 .y^2 = 2.xy= 2.6 =12
Vậy P min =12 dấu = xảy ra khi x^2=y^2 <=> x=y
( thông cảm mình gõ mũ ko đc )
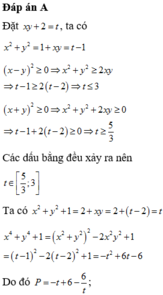
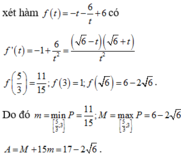
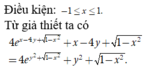
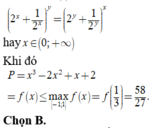
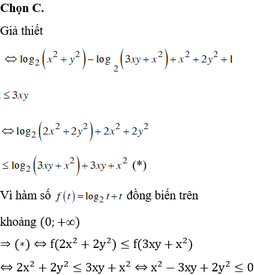
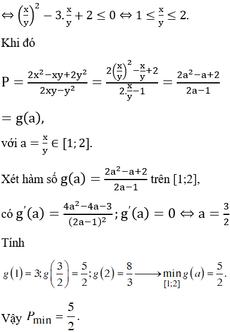
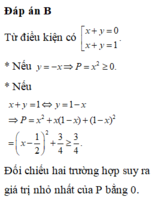
Giả thiết cho ta \(\left(x^2+y^2\right)^2+x^2+2y^2=3.\) Đặt \(t=x^2+y^2\) (ta có \(t\ge0\)).
Giá trị lớn nhất: Từ giả thiết ta suy ra \(t^2+t=3-y^2\le3\to\left(t+\frac{1}{2}\right)^2\le3+\frac{1}{4}\to t\le\frac{\sqrt{13}-1}{2}\)
Dấu bằng xảy ra khi và chỉ \(y=0,x=\pm\sqrt{\frac{\sqrt{13}-1}{2}}\). Vậy giá trị lớn nhất của \(B=t\) là \(\frac{\sqrt{13}-1}{2}.\)
Giá trị bé nhất: Từ giả thiết \(t^2+2t=3+x^2\ge3\to\left(t+1\right)^2\ge4\to t+1\ge2\to t\ge1.\) Dấu bằng xảy ra khi \(x=0,y=\pm1\). Vậy giá trị bé nhất của \(B=t\) là \(1.\)
okchu alna